簡介 Intro

此演算法是由 Joseph M. Morris 在 1979 年的論文「Traversing Binary Trees Simply and Cheaply」首次提出，因此稱之為 -- Morris traversal。其核心概念是利用樹中的空閒指針，縮減空間複雜度到常數。Morris traversal 主要是中序處理，但是修改後也是可以適用於前序和後序。

中序 In-Order

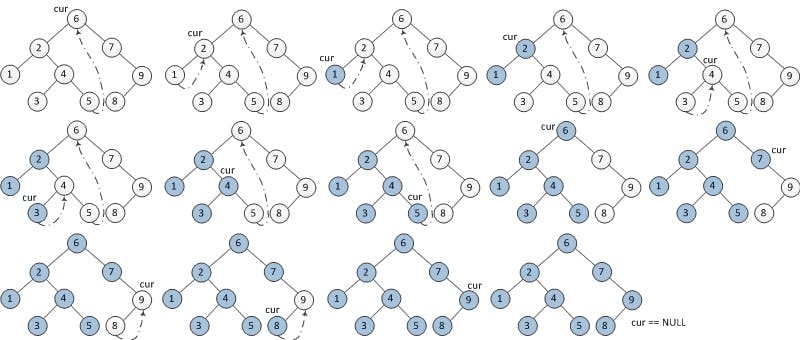
1. 先初始化 root 作為當前節點 curr

2. 當前節點 curr 不是 NULL 的時候，就往左子樹走

   • 當沒有左子樹的時候，就 輸出 curr 並將其 curr 設定為右節點

       if curr.left is None:
           print(curr)
           curr = curr.right
     

   • 當有左子樹時，在這個左子樹中找出最右側的節點 rightmost

     • 如果其右側節點為當前節點 curr，就將右節點設定為 NULL(還原樹的結構)，輸出 curr 並將 curr 設定為 curr 的右節點

         if rightmost.right == curr:
             rightmost.right = None
             print(curr)
             curr = curr.right
       

     • 如果 rightmost 沒有右節點的話，將其右節點指向為 curr，再將 curr 更新為左節點

         if rightmost.right is None:
             rightmost.right = curr
             curr = curr.left
       

3. 重複步驟一和二直到 curr 等於 NULL

def inorder(root):
    curr = root

    while curr:
        if curr.left:
            prev = curr.left

            while prev.right and prev.right != curr:
                prev = prev.right

            if prev.right:
                prev.right = None
                yield curr.val
                curr = curr.right
            else:
                prev.right = curr
                curr = curr.left
        else:
            yield curr.val
            curr = curr.right

前序 Pre-Order

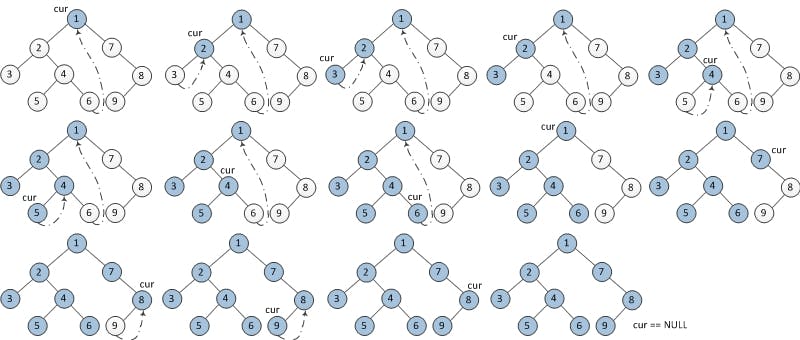
與中序基本上相同，唯一不同的地方在於輸出的順序

1. 先初始化 root 作為當前節點 curr

2. 當前節點 curr 不是 NULL 的時候，就往左子樹走

   • 當沒有左子樹的時候，就 輸出 curr 並將其 curr 設定為右節點

       if curr.left is None:
           curr = curr.right
     

   • 當有左子樹時，在這個左子樹中找出最右側的節點 rightmost

     • 如果 rightmost 的右側節點為當前節點 curr，就將其設定為 NULL(還原樹的結構)，將 curr 設定為 curr 的右節點

         if rightmost.right == curr:
             rightmost.right = None
             curr = curr.right
       

     • 如果 rightmost 沒有右節點的話，將其右節點指向為 curr後輸出 curr，再將 curr 更新為左節點

         if rightmost.right is None:
             rightmost.right = curr
             print(curr)   # 這邊跟 inorder 不同的地方
             curr = curr.left
       

3. 重複步驟一和二直到 curr 等於 NULL

前序是在做連結的時候(rightmost.right = curr)時輸出

中序則是在還原樹(rightmost.right = None)的時候輸出

def preorder(root):
    curr = root

    while curr:
        if curr.left:
            prev = curr.left

            while prev.right and prev.right != curr:
                prev = prev.right

            if prev.right:
                prev.right = None
                curr = curr.right
            else:
                yield curr.val
                prev.right = curr
                curr = curr.left
        else:
            yield curr.val
            curr = curr.right

後序 Post-Order

後續則稍顯複雜，可以有兩種方式。第一種是使用多增加一個臨時節點 temp，並設定 root 為其左節點。第二種則是將原本的條件轉換成右節點

添加臨時節點

1. 將 temp 設定為 curr

2. 當前節點 curr 不是 NULL 的時候，就往左子樹走

   • 當沒有左子樹的時候，將其 curr 設定為右節點

       if curr.left is None:
           curr = curr.right
     

   • 當有左子樹時，在這個左子樹中找出最右側的節點rightmost

     • 如果rightmost的右節點為當前節點 curr，就將其設定為 NULL(還原樹的結構)。倒序輸出 curr 的左子樹節點到 rightmost 的所有節點。將 curr 設定為 curr 的右節點

         if rightmost.right == curr:
             rightmost.right = None
             reverse(curr.left)
             curr = curr.right
       

     • 如果rightmost的沒有右節點，將其右節點指向為 curr後，再將 curr 更新為左節點

         if rightmost.right is None:
             rightmost.right = curr
             curr = curr.left
       

3. 重複步驟一和二直到 curr 等於 NULL

def reverse(node):
    tmp = []
    while node:
        tmp.append(node.val)
        node = node.right
    for val in range(reversed(tmp)):
        yield val

def postorder(root):
    curr = root

    while curr:
        if curr.left:
            prev = curr.left

            while prev.right and prev.right != curr:
                prev = prev.right

            if prev.right:
                prev.right = None
                reverse(curr.left)
            else:
                prev.right = curr
                curr = curr.left
        else:
            curr = curr.right
    reverse(root)

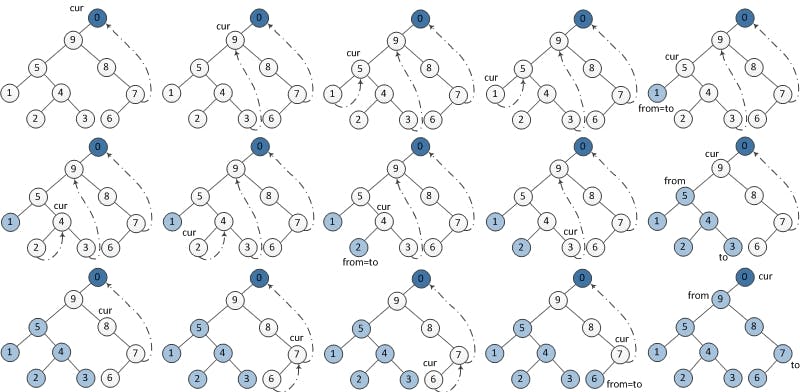
條件轉換

1. 先初始化 root 作為當前節點 curr

2. 當前節點 curr 不是 NULL 的時候，就往左子樹走

   • 當沒有右子樹的時候，就 輸出 curr 並將其 curr 設定為左節點
     curr = curr -> left

       if curr.right is None:
           print(curr)
           curr = curr.left
     

   • 當有右子樹時，在這個右子樹中找出最左側的節點 leftmost

     • 如果其 leftmost 的左節點為當前節點 curr，就將其設定為 NULL(還原樹的結構)，並將 curr 設定為 curr 的左節點
       leftmost -> left = NULL, curr = curr -> left

         if leftmost.left == curr:
             leftmost.left = None
             curr = curr.left
       

     • 如果 leftmost 沒有左節點的話，將其左節點指向為 curr並 輸出 curr ，再將 curr 更新為右節點 leftmost -> left = curr, curr = curr -> right

         if leftmost.left is None:
             leftmost.left = curr
             print(curr)
             curr = curr.right
       

3. 重複步驟一和二直到 curr 等於 NULL

def postorder(root):
    curr = root

    while curr:
        if curr.right:
            prev = curr.right

            while prev.left and prev.left != curr:
                prev = prev.left

            if prev.left:
                prev.left = None
                curr = curr.left
            else:
                yield curr.val
                prev.left = curr
                curr = curr.right
        else:
            yield curr.val
            curr = curr.left

Reference

• Stack overflow: Explain Morris inorder tree traversal without using stacks or recursion

• Morris Traversal方法遍历二叉树（非递归，不用栈，O(1)空间）

• 莫里斯遍历