141. Linked List Cycle
題目敘述
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
Example 1:
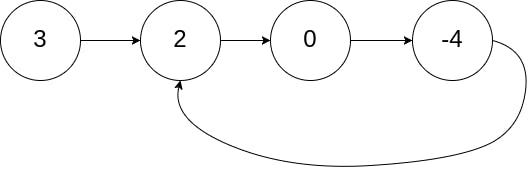
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
Example 2:
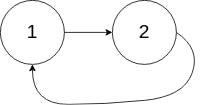
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.
Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range
[0, 10**4]. -10**5 <= Node.val <= 10**5posis-1or a valid index in the linked-list.
Follow up: Can you solve it using O(1) (i.e. constant) memory?
題目翻譯
嘗試在空間複雜度是常數的情況下解題。
今天給一個序列 head,判斷此序列是否有迴圈行程。使用 next 來接觸下一個節點。pos 表示其迴圈連接的點。
解法解析
解法主要有兩種,第一種就是消耗空間複雜度,用 Hash Table 的方式來記錄已經判斷過的節點。 第二種方式就是使用類似 Floyd 龜兔演算法的方式來判斷是否有迴圈,也可算是一種 Two-Pointer 解法。這邊要特別提到的是 PHP 的檢查有點問題,會一直測試不過。
解法範例
Go
Hash Table
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func hasCycle(head *ListNode) bool {
var nodesSeen = make(map[*ListNode]bool)
for head != nil {
if nodesSeen[head] {
return true
}
nodesSeen[head] = true
head = head.Next
}
return false
}
Floyd's Cycle Finding Algorithm
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func hasCycle(head *ListNode) bool {
if head == nil {
return false
}
var slow *ListNode = head
var fast *ListNode = head.Next
for slow != fast {
if fast == nil || fast.Next == nil {
return false
}
slow = slow.Next
fast = fast.Next.Next
}
return true
}
JavaScript
Hash Table
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
*/
var hasCycle = function (head) {
const nodesSeen = new Set();
while (head) {
if (nodesSeen.has(head)) {
return true;
}
nodesSeen.add(head);
head = head.next;
}
return false;
};
Floyd's Cycle Finding Algorithm
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
*/
var hasCycle = function (head) {
if (!head) {
return false;
}
let slow = head;
let fast = head.next;
while (slow !== fast) {
if (!fast || !fast.next) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
};
Kotlin
Hash Table
/**
* Example:
* var li = ListNode(5)
* var v = li.`val`
* Definition for singly-linked list.
* class ListNode(var `val`: Int) {
* var next: ListNode? = null
* }
*/
class Solution {
fun hasCycle(head: ListNode?): Boolean {
var nodesSeen = mutableSetOf<ListNode>()
var node = head
while (node != null) {
if (nodesSeen.contains(node)) {
return true
}
nodesSeen.add(node)
node = node.next
}
return false
}
}
Floyd's Cycle Finding Algorithm
/**
* Example:
* var li = ListNode(5)
* var v = li.`val`
* Definition for singly-linked list.
* class ListNode(var `val`: Int) {
* var next: ListNode? = null
* }
*/
class Solution {
fun hasCycle(head: ListNode?): Boolean {
if (head == null) return false
var slow = head
var fast = head.next
while (slow != fast) {
if (fast == null || fast.next == null) return false
slow = slow?.next
fast = fast?.next?.next
}
return true
}
}
PHP
Hash Table
/**
* Definition for a singly-linked list.
* class ListNode {
* public $val = 0;
* public $next = null;
* function __construct($val) { $this->val = $val; }
* }
*/
class Solution
{
/**
* @param ListNode $head
* @return Boolean
*/
function hasCycle($head)
{
$nodesSeen = [];
while (!is_null($head)) {
if (in_array($head, $nodesSeen)) {
return true;
}
$nodesSeen[] = $head;
$head = $head->next;
}
return false;
}
}
Floyd's Cycle Finding Algorithm
/**
* Definition for a singly-linked list.
* class ListNode {
* public $val = 0;
* public $next = null;
* function __construct($val) { $this->val = $val; }
* }
*/
class Solution
{
/**
* @param ListNode $head
* @return Boolean
*/
function hasCycle($head)
{
if (is_null($head)) {
return false;
}
$slow = $head;
$fast = $head->next;
while ($slow !== $fast) {
if (is_null($fast) || is_null($fast->next)) {
return false;
}
$slow = $slow->next;
$fast = $fast->next->next;
}
return true;
}
}
Python
Hash Table
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: ListNode | None) -> bool:
nodes_seen: set[ListNode] = set()
while head is not None:
if head in nodes_seen:
return True
nodes_seen.add(head)
head = head.next
return False
Floyd's Cycle Finding Algorithm
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def hasCycle(self, head: ListNode | None) -> bool:
if head is None:
return False
slow: ListNode = head
fast: ListNode = head.next
while slow != fast:
if fast is None or fast.next is None:
return False
slow = slow.next
fast = fast.next.next
return True
Rust
Swift
Hash Table
/**
* Definition for singly-linked list.
* public class ListNode {
* public var val: Int
* public var next: ListNode?
* public init(_ val: Int) {
* self.val = val
* self.next = nil
* }
* }
*/
class Solution {
func hasCycle(_ head: ListNode?) -> Bool {
var nodesSeen = [ListNode]()
var node = head
while node != nil {
if nodesSeen.contains(where: {$0 === node!}) {
return true
}
nodesSeen.append(node!)
node = node?.next
}
return false
}
}
Floyd's Cycle Finding Algorithm
/**
* Definition for singly-linked list.
* public class ListNode {
* public var val: Int
* public var next: ListNode?
* public init(_ val: Int) {
* self.val = val
* self.next = nil
* }
* }
*/
class Solution {
func hasCycle(_ head: ListNode?) -> Bool {
guard head != nil else {
return false
}
var slow: ListNode? = head
var fast: ListNode? = head?.next
while slow !== fast {
if fast == nil || fast?.next == nil {
return false
}
slow = slow?.next
fast = fast?.next?.next
}
return true
}
}
