941. Valid Mountain Array

題目敘述

Given an array of integers arr, return true if and only if it is a valid mountain array.

Recall that arr is a mountain array if and only if:

• arr.length >= 3
• There exists some i with 0 < i < arr.length - 1 such that:
  • arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
  • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

Example 1:

Input: arr = [2,1]
Output: false

Example 2:

Input: arr = [3,5,5]
Output: false

Example 3:

Input: arr = [0,3,2,1]
Output: true

Constraints:

• 1 <= arr.length <= 10^4
• 0 <= arr[i] <= 10^4

Hint 1:

It's very easy to keep track of a monotonically increasing or decreasing ordering of elements. You just need to be able to determine the start of the valley in the mountain and from that point onwards, it should be a valley i.e. no mini-hills after that. Use this information in regards to the values in the array and you will be able to come up with a straightforward solution.

題目翻譯

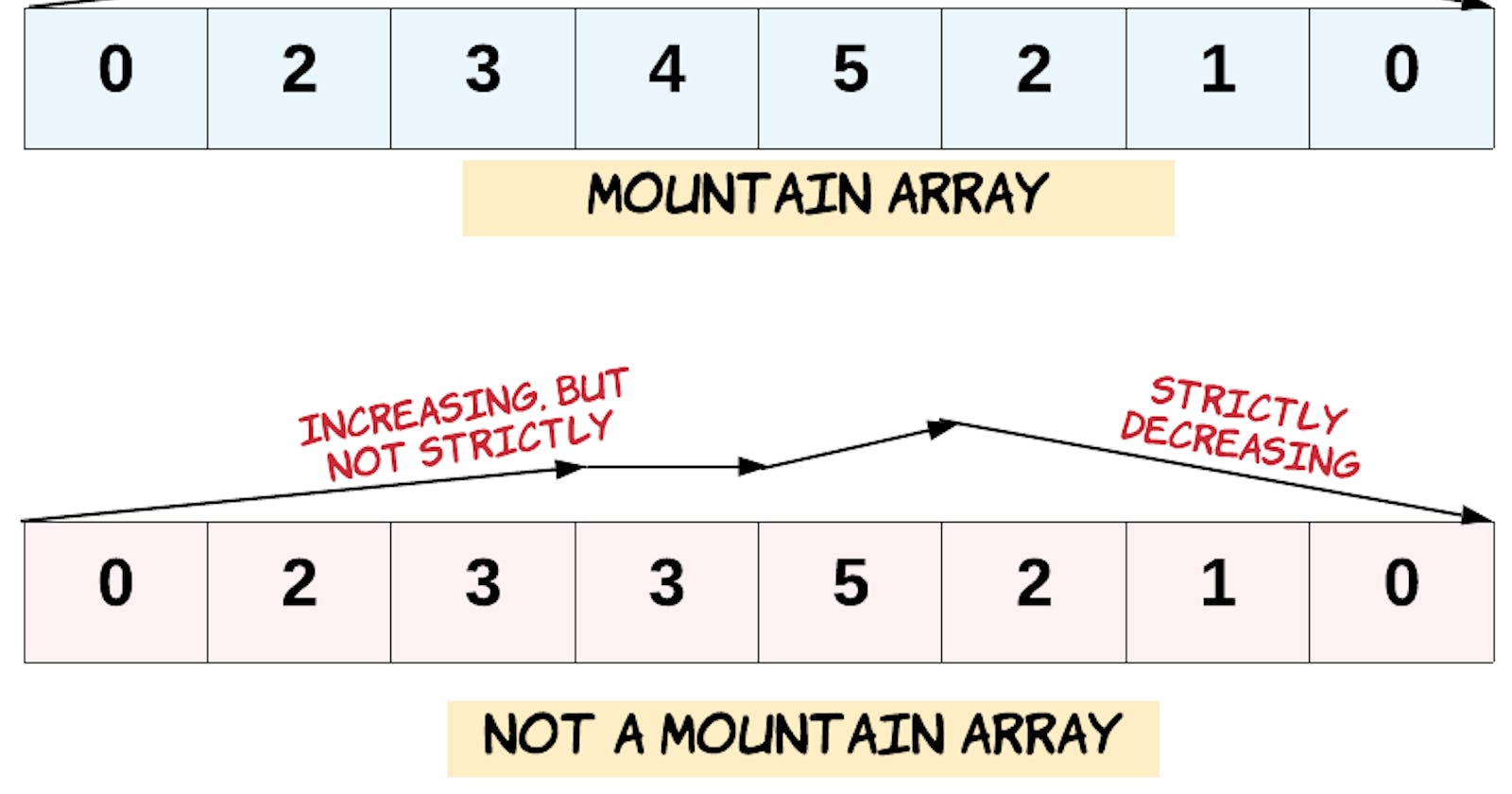
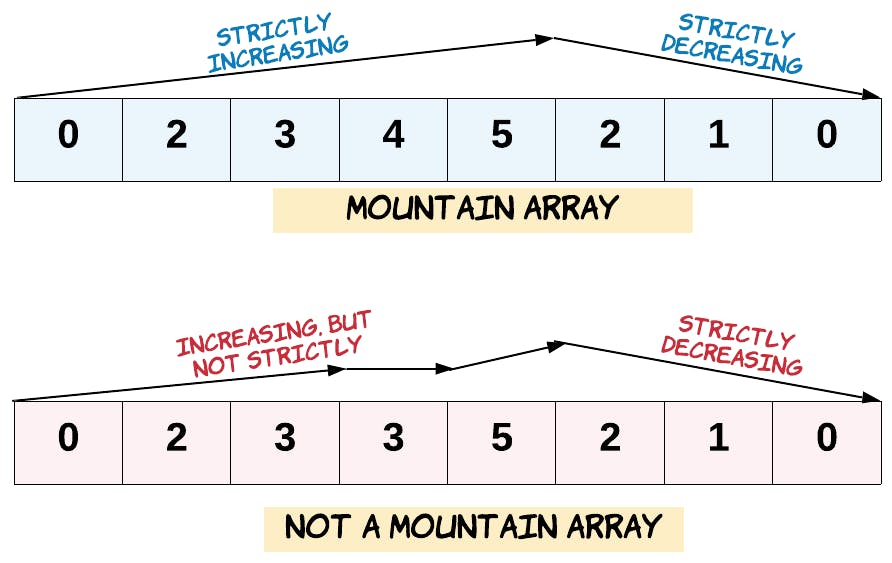
這邊會給一個參數 arr，然後題目希望去判斷這個 arr 是不是一個 "山形陣列"。然後按照定義，需要從頭尾往中間的數字要越來越高，不能有同數值。

解法解析

算是滿簡單的題目，可以先略過 arr 長度小於 3 的。因為不管怎樣都不符合 "山形陣列" 的定義，[1, 2] 或 [2, 1] 都不對。所以可以先略過。之後從開頭往結尾找，中間有同數值的話就中斷回傳 false。發現到最高點後判斷是不是到結尾了，如果是就中斷回傳 false。然後再開始判斷是不是數值往下了。所以總共用了兩個迴圈處理。

• Time：O(n)
• Space：O(1)

程式範例

Python

class Solution:
    def validMountainArray(self, arr: List[int]) -> bool:
        N = len(arr)
        if N < 3:
            return False
        i = 0

        # walk up
        while i+1 < N and arr[i] < arr[i+1]:
            i += 1

        # peak can't be first or last
        if i == 0 or i == N-1:
            return False

        # walk down
        while i+1 < N and arr[i] > arr[i+1]:
            i += 1

        return i == N-1

JavaScript

/**
 * @param {number[]} arr
 * @return {boolean}
 */
var validMountainArray = function(arr) {
    const N = arr.length;
    if (N < 3) return false;
    let i = 0;

    while (i < N - 1 && arr[i] < arr[i + 1]) i++;

    if (i === 0 || i === N - 1) return false;

    while (i < N - 1 && arr[i] > arr[i + 1]) i++;

    return i === N - 1;
};

Go

func validMountainArray(arr []int) bool {
    N := len(arr)
    if N < 3 {
        return false
    }
    i := 0

    for i < N-1 && arr[i] < arr[i+1] {
        i++
    }

    if i == 0 || i == N-1 {
        return false
    }

    for i < N-1 && arr[i] > arr[i+1] {
        i++
    }

    return i == N-1
}

Swift

class Solution {
    func validMountainArray(_ arr: [Int]) -> Bool {
        let N = arr.count
        guard N > 2 else { return false }
        var i = 0
        while i < N - 1 && arr[i] < arr[i + 1] {
            i += 1
        }
        if i == 0 || i == N - 1 {
            return false
        }
        while i < N - 1 && arr[i] > arr[i + 1] {
            i += 1
        }
        return i == N - 1
    }
}

Kotlin

class Solution {
    fun validMountainArray(arr: IntArray): Boolean {
        var N = arr.size
        if (N < 3) return false
        var i = 0
        while (i < N - 1 && arr[i] < arr[i + 1]) {
            i++
        }
        if (i == 0 || i == N - 1) return false
        while (i < N - 1 && arr[i] > arr[i + 1]) {
            i++
        }
        return i == N - 1
    }
}

PHP

class Solution
{

    /**
     * @param Integer[] $arr
     * @return Boolean
     */
    function validMountainArray($arr)
    {
        $N = count($arr);
        if ($N < 3) {
            return false;
        }
        $i = 0;
        while ($i < $N - 1 && $arr[$i] < $arr[$i + 1]) {
            $i++;
        }
        if ($i == 0 || $i == $N - 1) {
            return false;
        }
        while ($i < $N - 1 && $arr[$i] > $arr[$i + 1]) {
            $i++;
        }
        return $i == $N - 1;
    }
}