882. Reachable Nodes In Subdivided Graph

題目敘述

You are given an undirected graph (the "original graph") with n nodes labeled from 0 to n - 1. You decide to subdivide each edge in the graph into a chain of nodes, with the number of new nodes varying between each edge.

The graph is given as a 2D array of edges where edges[i] = [ui, vi, cnti] indicates that there is an edge between nodes ui and vi in the original graph, and cnti is the total number of new nodes that you will subdivide the edge into. Note that cnti == 0 means you will not subdivide the edge.

To subdivide the edge [ui, vi], replace it with (cnti + 1) new edges and cnti new nodes. The new nodes are x1, x2, ..., xcnti, and the new edges are [ui, x1], [x1, x2], [x2, x3], ..., [xcnti+1, xcnti], [xcnti, vi].

In this new graph, you want to know how many nodes are reachable from the node 0, where a node is reachable if the distance is maxMoves or less.

Given the original graph and maxMoves, return the number of nodes that are reachable from node 0 in the new graph.

Example 1:

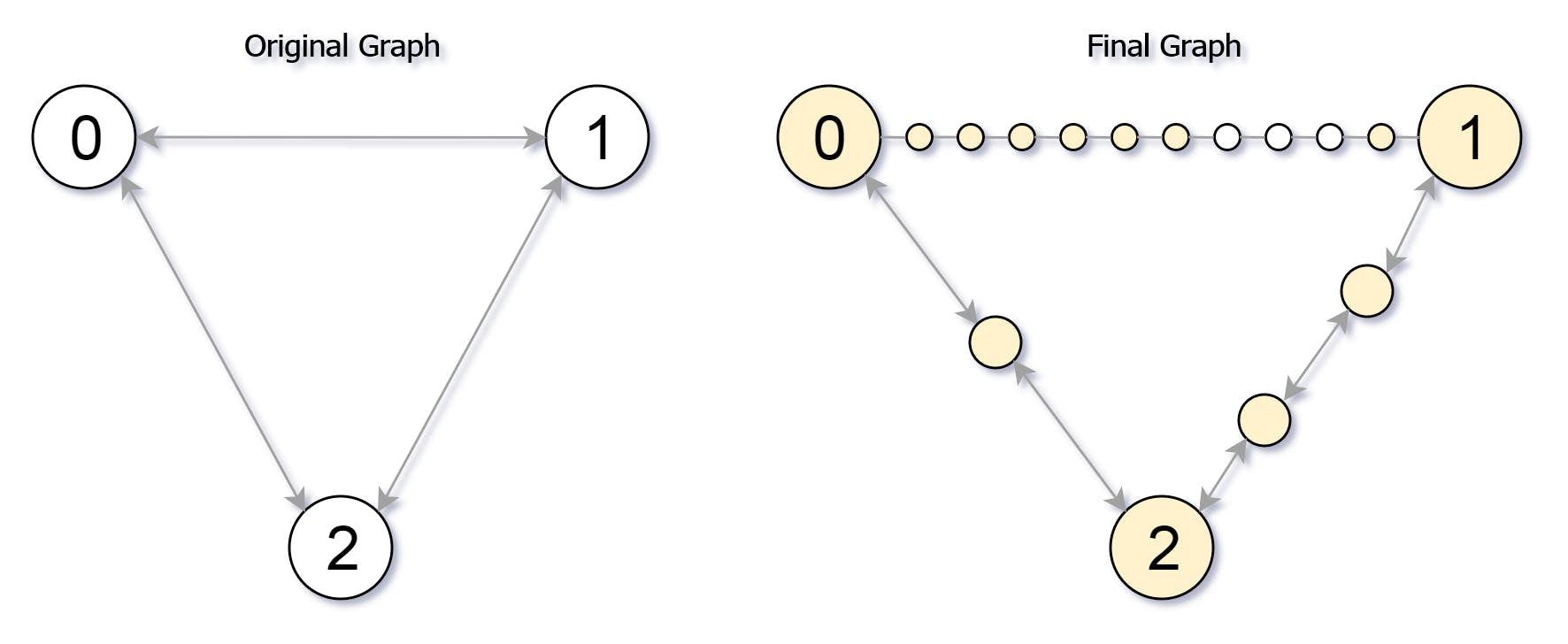
Input: edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
Output: 13
Explanation: The edge subdivisions are shown in the image above.
The nodes that are reachable are highlighted in yellow.

Example 2:

Input: edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4
Output: 23

Example 3:

Input: edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5
Output: 1
Explanation: Node 0 is disconnected from the rest of the graph, so only node 0 is reachable.

Constraints:

• 0 <= edges.length <= min(n * (n - 1) / 2, 104)
• edges[i].length == 3
• 0 <= ui < vi < n
• There are no multiple edges in the graph.
• 0 <= cnti <= 104
• 0 <= maxMoves <= 109
• 1 <= n <= 3000

題目翻譯

此題就是有一個無方向的路徑圖，有 n 個節點。然後會在這路徑圖中插入一些新的節點，其節點的關係會儲存在 edges 中，元素關係為 [u, v, cnt]，u 和 v 是兩個點節，cnt 是指插入多少新的節點。以範例一的圖來說 [0, 1, 10] 指的就是在節點 0 和 1 之間插入 10 個新節點。題目要找出的就是，從節點 0 開始，走 maxMoves 可以經過哪些節點。

解法解析

這題的解法主要使用了 Dijkstra 演算法，這是一個著名的計算最短路徑問題的演算法，可以找出起點到終點之間，計算權重總和最小的路徑。而且只適用於權重無負值的情境，所以剛好是好適用此題目。 第一步先宣告初始化的 graph，記錄個節點之間的關係。 再來這邊使用的是 Min Heap，每次的迴圈中取出最小值。

程式範例

JavaScript

/**
 * @param {number[][]} edges
 * @param {number} maxMoves
 * @param {number} n
 * @return {number}
 */
var reachableNodes = function (edges, maxMoves, n) {
    const graph = {};
    for (let [u, v, w] of edges) {
        if (!(u in graph)) graph[u] = {};
        if (!(v in graph)) graph[v] = {};
        graph[u][v] = graph[v][u] = w;
    }

    const pq = new MinPriorityQueue({ priority: (x) => x[0] });
    pq.enqueue([0, 0]);
    const dist = { 0: 0 };
    const used = {};
    let ans = 0;

    while (pq.size()) {
        const [d, node] = pq.dequeue().element;
        if (d > dist[node]) continue;
        ans += 1;

        for (const nei in graph[node]) {
            const weight = graph[node][nei];
            const v = Math.min(weight, maxMoves - d);
            used[`${node},${nei}`] = v;

            const d2 = d + weight + 1;
            if (d2 < (dist?.[nei] ?? maxMoves + 1)) {
                pq.enqueue([d2, nei]);
                dist[nei] = d2;
            }
        }
    }

    for (const [u, v, w] of edges) {
        ans += Math.min(
            w,
            (used?.[`${u},${v}`] ?? 0) + (used?.[`${v},${u}`] ?? 0)
        );
    }
    return ans;
};

Python

class Solution:
    def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
        graph = collections.defaultdict(dict)
        for u, v, w in edges:
            graph[u][v] = graph[v][u] = w

        pq = [(0, 0)]
        dist = {0: 0}
        used = {}
        ans = 0

        while pq:
            d, node = heapq.heappop(pq)
            if d > dist[node]:
                continue
            # Each node is only visited once.  We've reached
            # a node in our original graph.
            ans += 1

            for nei, weight in graph[node].items():
                # maxMoves - d is how much further we can walk from this node;
                # weight is how many new nodes there are on this edge.
                # v is the maximum utilization of this edge.
                v = min(weight, maxMoves - d)
                used[node, nei] = v

                # d2 is the total distance to reach 'nei' (neighbor) node
                # in the original graph.
                d2 = d + weight + 1
                if d2 < dist.get(nei, maxMoves+1):
                    heapq.heappush(pq, (d2, nei))
                    dist[nei] = d2

        # At the end, each edge (u, v, w) can be used with a maximum
        # of w new nodes: a max of used[u, v] nodes from one side,
        # and used[v, u] nodes from the other.
        for u, v, w in edges:
            ans += min(w, used.get((u, v), 0) + used.get((v, u), 0))

        return ans

Reference

• zhuanlan.zhihu.com/p/63395403
• cnblogs.com/goldsunshine/p/12978305.html