1007. Minimum Domino Rotations For Equal Row

題目敘述

In a row of dominoes, tops[i] and bottoms[i] represent the top and bottom halves of the i**th domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the i**th domino, so that tops[i] and bottoms[i] swap values.

Return the minimum number of rotations so that all the values in tops are the same, or all the values in bottoms are the same.

If it cannot be done, return -1.

Example 1:

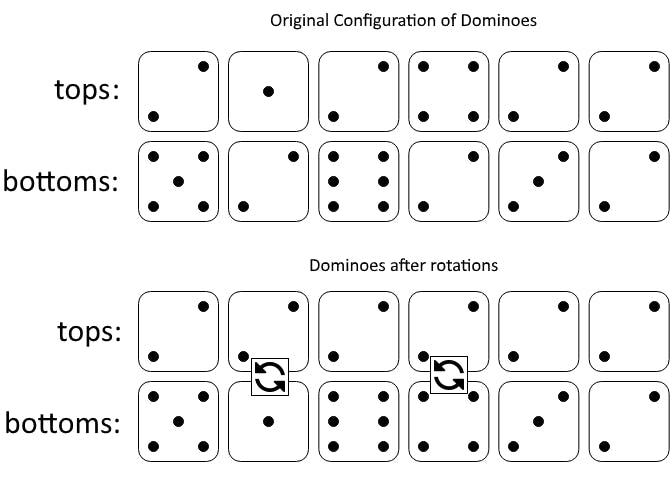
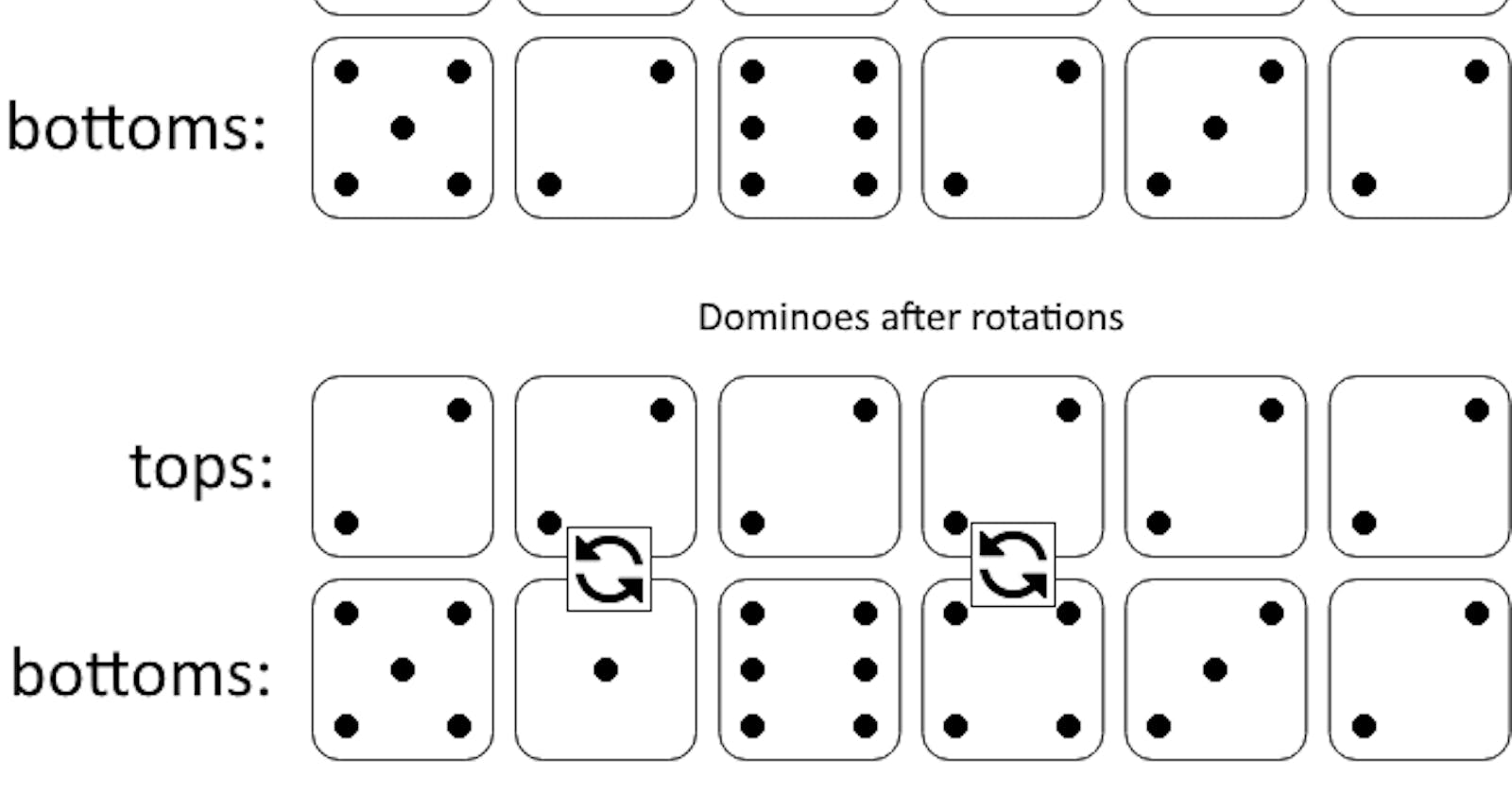
Input: tops = [2,1,2,4,2,2], bottoms = [5,2,6,2,3,2]
Output: 2
Explanation:
The first figure represents the dominoes as given by tops and bottoms: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: tops = [3,5,1,2,3], bottoms = [3,6,3,3,4]
Output: -1
Explanation:
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

• 2 <= tops.length <= 2 * 10**4
• bottoms.length == tops.length
• 1 <= tops[i], bottoms[i] <= 6

題目翻譯

這題是有一組骨牌拆成上下兩部分，分別儲存在 tops 和 bottoms，其中用 tops[i] 和 bottoms[i] 來表示對應的值。再來是我們可以互換 tops[i] 和 bottoms[i] 的值，題目要找出如果最小互換次數，可以讓 tops 或 bottoms 的值都相同的情況。如果沒這種情況就回傳 -1。

解法解析

解題的概念是，如果要可以達成相同值的狀況，代表在同 i 欄位一定要有一個值是可以達到條件的，所以先取 tops[0] 當代表去做判斷。

1. 先判斷在不在 tops 和 bottoms 中
2. 分別計算在 tops 和 bottoms 需要替換的次數
3. 回傳 step2 中的最小值(tops 還是 bottoms 的替換次數最少的)
4. 如果是 -1 那就換成用 bottoms[0] 當代表判斷

解法範例

Go

func minDominoRotations(tops []int, bottoms []int) int {
    rotations := check(tops, bottoms, tops[0])
    if rotations != -1 || tops[0] == bottoms[0] {
        return rotations
    }
    return check(tops, bottoms, bottoms[0])
}

func check(tops, bottoms []int, x int) int {
    var rotationsA, rotationsB int

    for i := 0; i < len(tops); i++ {
        if tops[i] != x && bottoms[i] != x {
            return -1
        } else if tops[i] != x {
            rotationsA++
        } else if bottoms[i] != x {
            rotationsB++
        }
    }

    if rotationsA > rotationsB {
        return rotationsB
    }
    return rotationsA
}

JavaScript

/**
 * @param {number[]} tops
 * @param {number[]} bottoms
 * @return {number}
 */
var minDominoRotations = function (tops, bottoms) {
    const check = (x) => {
        let rotationsA = 0,
            rotationsB = 0;
        for (let i = 0; i < tops.length; i++) {
            if (tops[i] != x && bottoms[i] != x) return -1;
            else if (tops[i] != x) rotationsA++;
            else if (bottoms[i] != x) rotationsB++;
        }
        return Math.min(rotationsA, rotationsB);
    };

    const rotations = check(tops[0]);
    return rotations !== -1 || bottoms[0] === tops[0]
        ? rotations
        : check(bottoms[0]);
};

Kotlin

class Solution {
    fun minDominoRotations(tops: IntArray, bottoms: IntArray): Int {
        var rotations = check(tops, bottoms, tops[0])
        if (rotations != -1 || tops[0] == bottoms[0]) {
            return rotations

        }
        return check(tops, bottoms, bottoms[0])
    }

    private fun check(tops: IntArray, bottoms: IntArray, x: Int): Int {
        var rotationsA = 0
        var rotationsB = 0
        for (i in tops.indices) {
            if (tops[i] != x && bottoms[i] != x) return -1
            if (tops[i] != x) rotationsA++
            if (bottoms[i] != x) rotationsB++
        }
        return Math.min(rotationsA, rotationsB)
    }
}

PHP

class Solution
{

    /**
     * @param Integer[] $tops
     * @param Integer[] $bottoms
     * @return Integer
     */
    function minDominoRotations($tops, $bottoms)
    {
        $rotations = $this->check($tops, $bottoms, $tops[0]);
        if ($rotations !== -1 || $tops[0] == $bottoms[0]) {
            return $rotations;
        }
        return $this->check($tops, $bottoms, $bottoms[0]);
    }

    function check($tops, $bottoms, $x)
    {
        $rotations_a = $rotations_b = 0;
        for ($i = 0; $i < count($tops); $i++) {
            if ($tops[$i] != $x && $bottoms[$i] != $x) {
                return -1;
            } else if ($tops[$i] != $x) {
                $rotations_a++;
            } else if ($bottoms[$i] != $x) {
                $rotations_b++;
            }
        }
        return min($rotations_a, $rotations_b);
    }
}

Python

class Solution:
    def minDominoRotations(self, tops: List[int], bottoms: List[int]) -> int:
        def check(x):
            """
            Return min number of swaps
            if one could make all elements in tops or bottoms equal to x.
            Else return -1.
            """
            # how many rotations should be done
            # to have all elements in tops equal to x
            # and to have all elements in bottoms equal to x
            rotations_a = rotations_b = 0
            for i in range(n):
                # rotations couldn't be done
                if tops[i] != x and bottoms[i] != x:
                    return -1
                # tops[i] != x and bottoms[i] == x
                elif tops[i] != x:
                    rotations_a += 1
                # tops[i] == x and bottoms[i] != x
                elif bottoms[i] != x:
                    rotations_b += 1
            # min number of rotations to have all
            # elements equal to x in tops or bottoms
            return min(rotations_a, rotations_b)

        n = len(tops)
        rotations = check(tops[0])
        # If one could make all elements in tops or bottoms equal to tops[0]
        if rotations != -1 or tops[0] == bottoms[0]:
            return rotations
        # If one could make all elements in tops or bottoms equal to bottoms[0]
        return check(bottoms[0])

Rust

Swift

class Solution {
    func minDominoRotations(_ tops: [Int], _ bottoms: [Int]) -> Int {
        let rotations = check(tops[0], tops, bottoms)
        if rotations != -1 || tops[0] == bottoms[0] {
            return rotations
        }
        return check(bottoms[0], tops, bottoms)
    }

    private func check(_ x: Int, _ tops: [Int], _ bottoms: [Int]) -> Int {
        var rotationsA = 0, rotationsB = 0

        for i in 0..<tops.count {
            if tops[i] != x, bottoms[i] != x {
                return -1
            } else if  tops[i] != x {
                rotationsA += 1
            } else if bottoms[i] != x {
                rotationsB += 1
            }
        }
        return min(rotationsA, rotationsB)
    }
}