11. Container With Most Water

題目敘述

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the i**th line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

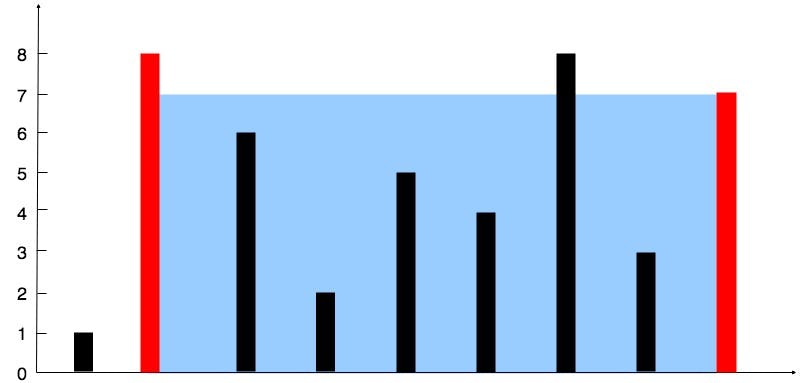
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1]
Output: 1

Constraints:

• n == height.length
• 2 <= n <= 10**5
• 0 <= height[i] <= 10**4

Hint 1:

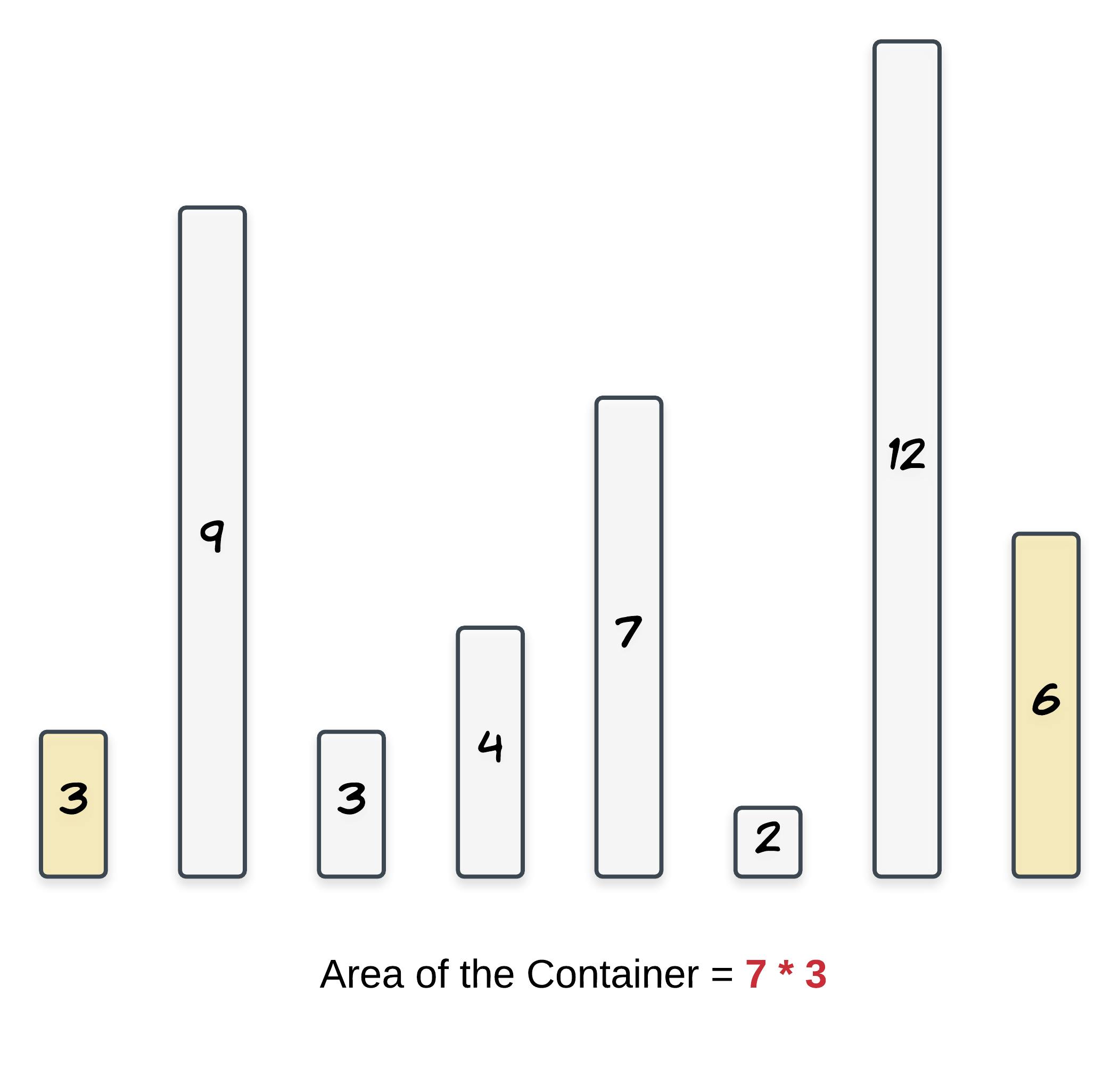
The aim is to maximize the area formed between the vertical lines. The area of any container is calculated using the shorter line as length and the distance between the lines as the width of the rectangle.

Area = length of shorter vertical line * distance between lines

We can definitely get the maximum width container as the outermost lines have the maximum distance between them. However, this container might not be the maximum in size as one of the vertical lines of this container could be really short.

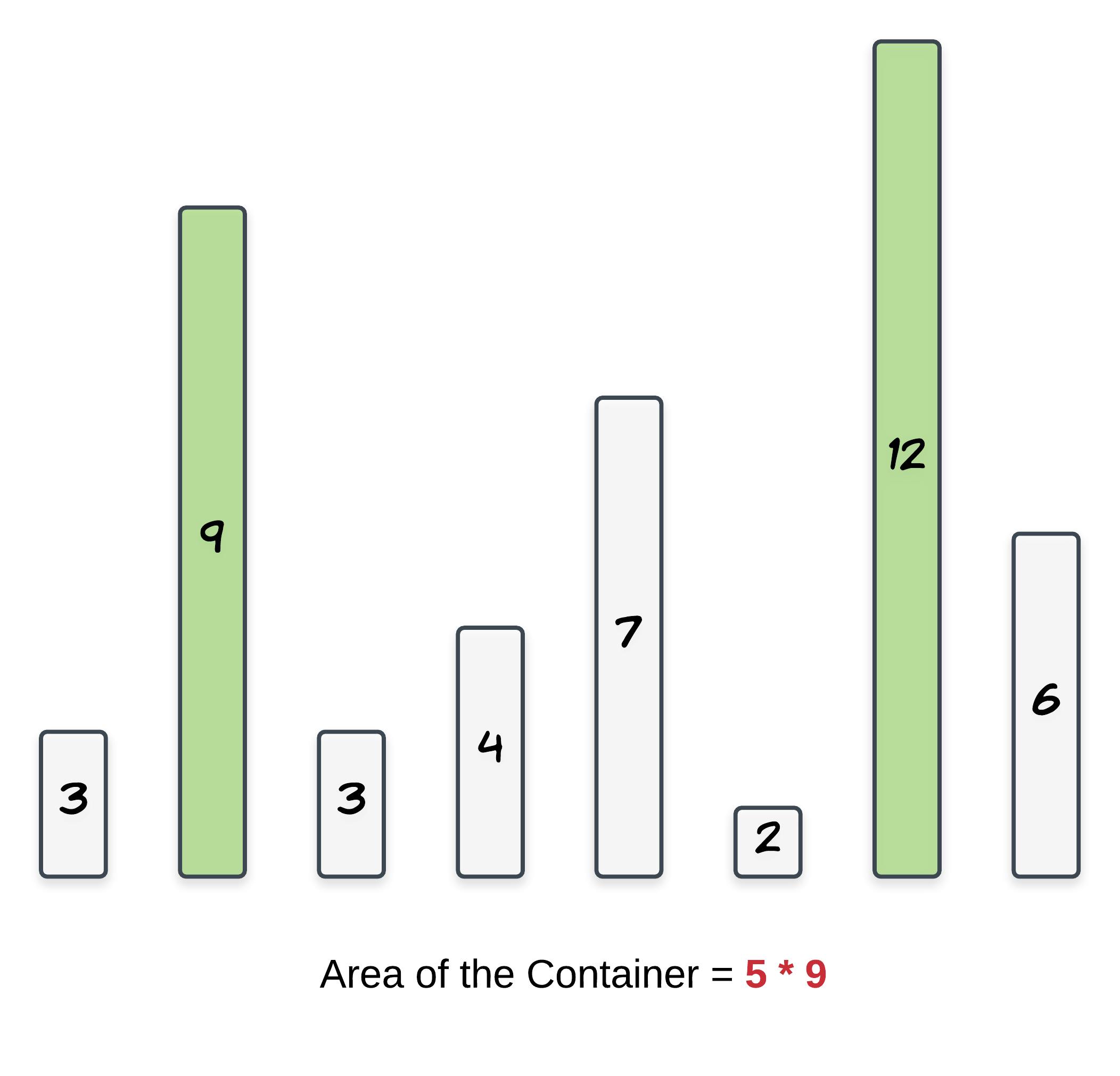
Hint 2:

Start with the maximum width container and go to a shorter width container if there is a vertical line longer than the current containers shorter line. This way we are compromising on the width but we are looking forward to a longer length container.

題目翻譯

這邊會給一個整數的陣列 height，是一串容器的高。要找出兩個高其中間的空間是最大的。

解法解析

這題是使用了 Two pointer 的解法，從開頭跟結尾往中間收斂，每次去比較容量的空間。

解法範例

Go

func maxArea(height []int) int {
    left, right, area := 0, len(height)-1, 0
    var vol int
    for left < right {
        if height[right] > height[left] {
            vol = (right - left) * height[left]
            left++
        } else {
            vol = (right - left) * height[right]
            right--
        }
        if vol > area {
            area = vol
        }
    }
    return area
}

JavaScript

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function (height) {
    let left = 0,
        right = height.length - 1,
        area = 0;

    while (left < right) {
        area = Math.max(
            area,
            Math.min(height[left], height[right]) * (right - left)
        );

        if (height[left] < height[right]) left++;
        else right--;
    }
    return area;
};

Kotlin

class Solution {
    fun maxArea(height: IntArray): Int {
        var left = 0
        var right = height.size - 1
        var area = 0
        while (left < right) {
            area = Math.max(area, Math.min(height[left], height[right]) * (right - left))
            if (height[left] < height[right]) left++ else right--
        }
        return area
    }
}

PHP

class Solution
{

    /**
     * @param Integer[] $height
     * @return Integer
     */
    function maxArea($height)
    {
        $area = 0;
        $left = 0;
        $right = count($height) - 1;

        while ($left < $right) {
            $area = max($area, min($height[$left], $height[$right]) * ($right - $left));
            if ($height[$left] < $height[$right]) {
                $left++;
            } else {
                $right--;
            }
        }
        return $area;
    }
}

Python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        area = 0
        left = 0
        right = len(height) - 1

        while left < right:
            area = max(area, min(
                height[left], height[right]) * (right - left))

            if height[right] > height[left]:
                left += 1
            else:
                right -= 1

        return area

Rust

Swift

class Solution {
  func maxArea(_ height: [Int]) -> Int {
    var left = 0
    var right = height.count - 1
    var area = 0

    while left < right {
      area = max(area, min(height[left], height[right]) * (right - left))

      if height[right] > height[left] {
        left += 1
      } else {
        right -= 1
      }
    }

    return area
  }
}