289. Game of Life

題目敘述

According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.

Example 1:

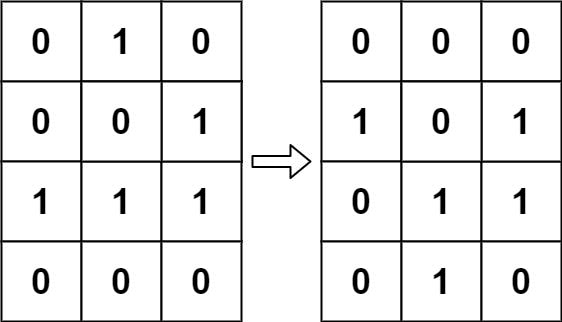
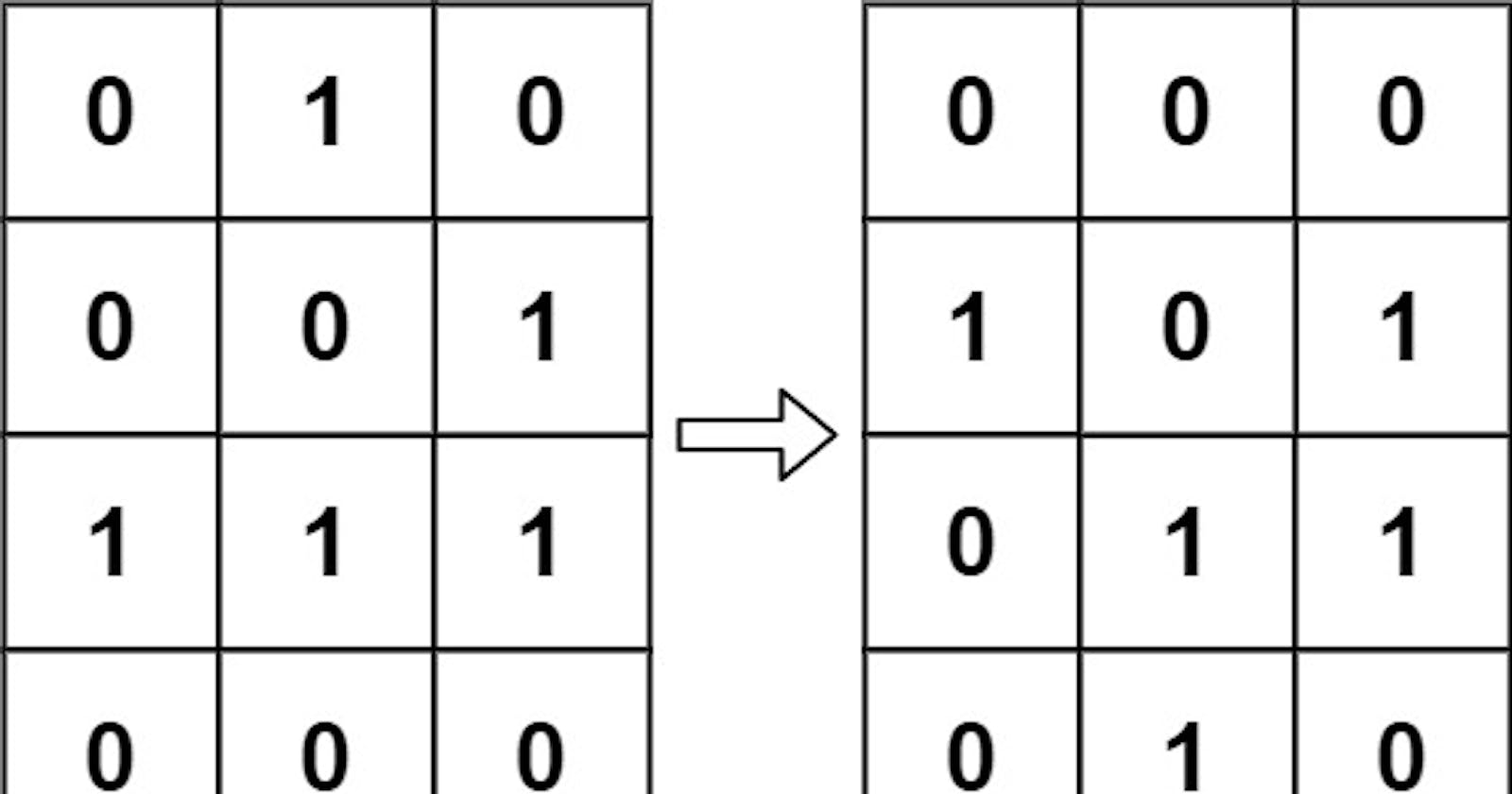
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

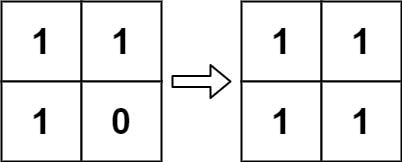
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 25
• board[i][j] is 0 or 1.

Follow up:

• Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
• In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?

題目翻譯

這題其實就是 Conway's Game of Life，寫出他的函式在 m x n 的二維矩陣中可以算出下一個盤面。具有四個條件：

1. 當前細胞為存活狀態時(1)，當周圍的存活細胞低於2個時（不包含2個），該細胞變成死亡狀態(0)。（模擬生命數量稀少）
2. 當前細胞為存活狀態時，當周圍有2個或3個存活細胞時，該細胞保持原樣。
3. 當前細胞為存活狀態時，當周圍有超過3個存活細胞時，該細胞變成死亡狀態。（模擬生命數量過多）
4. 當前細胞為死亡狀態時，當周圍有3個存活細胞時，該細胞變成存活狀態。（模擬繁殖）

解法解析

這個題目的解法是將其下一個棋盤的狀態儲存到另一個變數上，然後再利用 m x n 的迴圈去做每個 cell 的判斷。其中是在利用 neighbors 的變數去紀錄八個方向的操作，在每個 cell 作判斷的時候去判斷他的鄰居。

這邊有介紹一個額外的討論是，當這個棋盤範圍無限大呢？這樣要讓記憶體去記憶是不切實際的操作。然後再討論區就有的 Stefan Pochmann 就有提出優化的解法。就是我們只去找出棋盤中存活的細胞，只針對他們作判斷，不需要去記憶所有的狀態。

解法範例

Go

func gameOfLife(board [][]int) {
    neighbors := [][]int{
        {1, 0}, {1, -1}, {0, -1}, {-1, -1},
        {-1, 0}, {-1, 1}, {0, 1}, {1, 1},
    }

    var rows int = len(board)
    var cols int = len(board[0])

    for row := 0; row < rows; row++ {
        for col := 0; col < cols; col++ {
            liveNeighbors := 0
            for _, neighbor := range neighbors {
                r := row + neighbor[0]
                c := col + neighbor[1]

                if (r >= 0 && r < rows) && (c >= 0 && c < cols) && (board[r][c] == 1 || board[r][c] == -1) {
                    liveNeighbors++
                }
            }

            if board[row][col] == 1 && (liveNeighbors < 2 || liveNeighbors > 3) {
                board[row][col] = -1
            } else if board[row][col] == 0 && liveNeighbors == 3 {
                board[row][col] = 2
            }
        }
    }

    for row := 0; row < rows; row++ {
        for col := 0; col < cols; col++ {
            if board[row][col] > 0 {
                board[row][col] = 1
            } else {
                board[row][col] = 0
            }
        }
    }
}

JavaScript

/**
 * @param {number[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
var gameOfLife = function (board) {
    const neighbors = [
        [1, 0],
        [1, -1],
        [0, -1],
        [-1, -1],
        [-1, 0],
        [-1, 1],
        [0, 1],
        [1, 1],
    ];

    const rows = board.length,
        cols = board[0].length;
    for (let row = 0; row < rows; row++) {
        for (let col = 0; col < cols; col++) {
            let liveNeighbors = 0;
            for (const neighbor of neighbors) {
                const neighborRow = row + neighbor[0];
                const neighborCol = col + neighbor[1];
                if (
                    neighborRow >= 0 &&
                    neighborRow < rows &&
                    neighborCol >= 0 &&
                    neighborCol < cols &&
                    Math.abs(board[neighborRow][neighborCol]) === 1
                ) {
                    liveNeighbors++;
                }
            }
            if (
                board[row][col] === 1 &&
                (liveNeighbors < 2 || liveNeighbors > 3)
            ) {
                board[row][col] = -1;
            } else if (board[row][col] === 0 && liveNeighbors === 3) {
                board[row][col] = 2;
            }
        }
    }

    for (let row = 0; row < rows; row++) {
        for (let col = 0; col < cols; col++) {
            board[row][col] = board[row][col] > 0 ? 1 : 0;
        }
    }
};

Kotlin

PHP

Python

class Solution:
    def gameOfLife(self, board: List[List[int]]) -> None:
        """
        Do not return anything, modify board in-place instead.
        """
        # Neighbors array to find 8 neighboring cells for a given cell
        neighbors = [(1, 0), (1, -1), (0, -1), (-1, -1),
                     (-1, 0), (-1, 1), (0, 1), (1, 1)]

        rows = len(board)
        cols = len(board[0])

        # Iterate through board cell by cell.
        for row in range(rows):
            for col in range(cols):

                # For each cell count the number of live neighbors.
                live_neighbors = 0
                for neighbor in neighbors:

                    # row and column of the neighboring cell
                    r = (row + neighbor[0])
                    c = (col + neighbor[1])

                    # Check the validity of the neighboring cell and if it was originally a live cell.
                    if (r < rows and r >= 0) and (c < cols and c >= 0) and abs(board[r][c]) == 1:
                        live_neighbors += 1

                # Rule 1 or Rule 3
                if board[row][col] == 1 and (live_neighbors < 2 or live_neighbors > 3):
                    # -1 signifies the cell is now dead but originally was live.
                    board[row][col] = -1
                # Rule 4
                if board[row][col] == 0 and live_neighbors == 3:
                    # 2 signifies the cell is now live but was originally dead.
                    board[row][col] = 2

        # Get the final representation for the newly updated board.
        for row in range(rows):
            for col in range(cols):
                board[row][col] = 1 if board[row][col] > 0 else 0

Infinite board by Stefan Pochmann

from collections import Counter


class Solution:
    def gameOfLifeInfinite(self, live):
        ctr = Counter((I, J)
                      for i, j in live
                      for I in range(i-1, i+2)
                      for J in range(j-1, j+2)
                      if I != i or J != j)
        return {ij
                for ij in ctr
                if ctr[ij] == 3 or ctr[ij] == 2 and ij in live}

    def gameOfLife(self, board):
        live = {(i, j) for i, row in enumerate(board)
                for j, live in enumerate(row) if live}
        live = self.gameOfLifeInfinite(live)
        for i, row in enumerate(board):
            for j in range(len(row)):
                row[j] = int((i, j) in live)

Rust

Swift