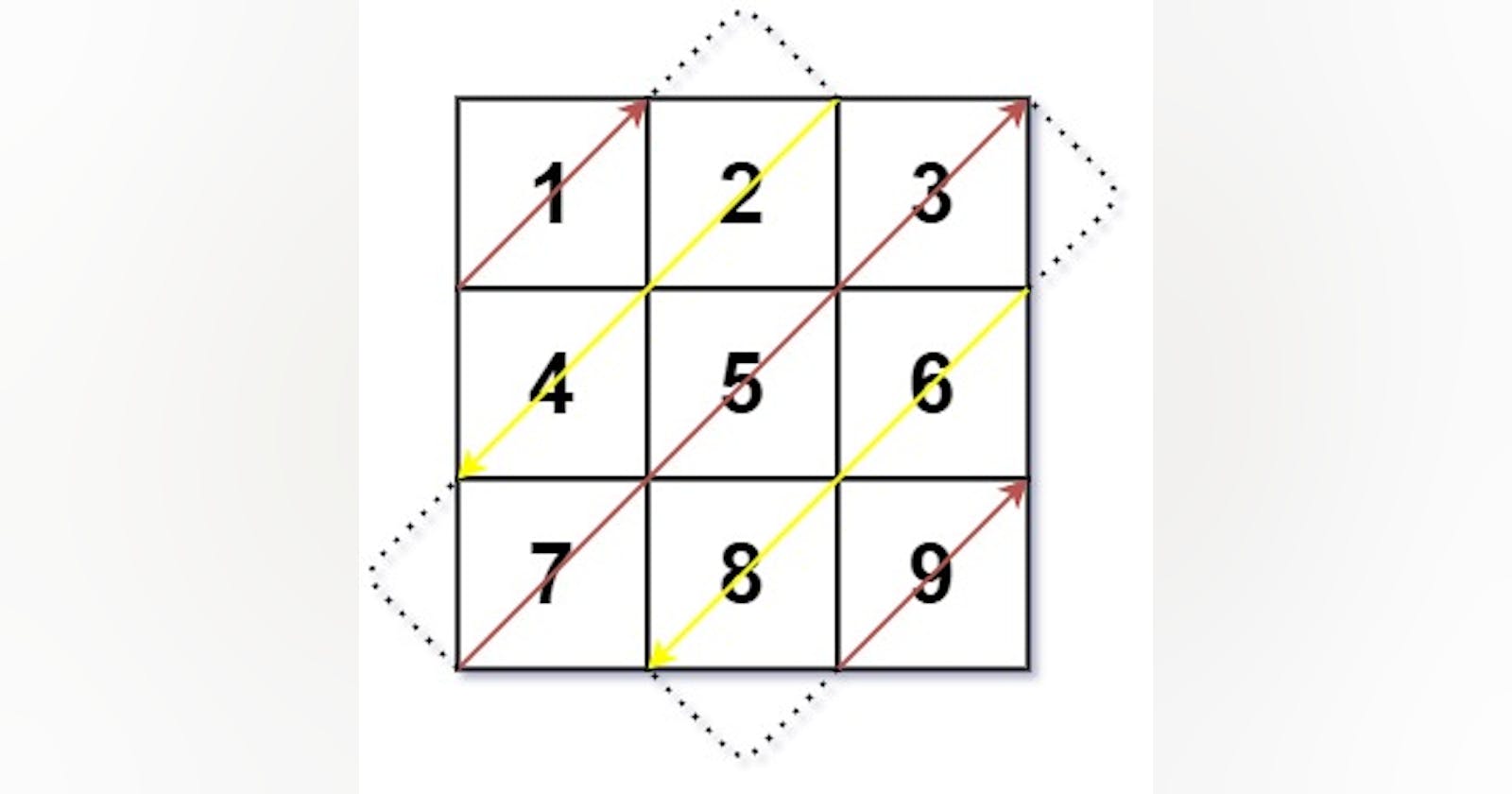
498. Diagonal Traverse

題目敘述

Given an m x n matrix mat, return an array of all the elements of the array in a diagonal order.

Example 1:

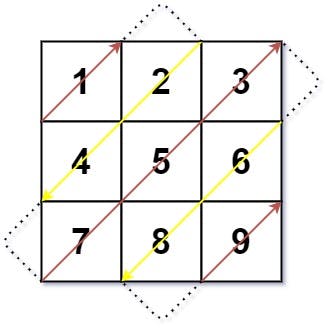
Input: mat = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,4,7,5,3,6,8,9]

Example 2:

Input: mat = [[1,2],[3,4]]
Output: [1,2,3,4]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 10**4
• 1 <= m * n <= 10**4
• -10**5 <= mat[i][j] <= 10**5

題目翻譯

這題目是想要在一個二維陣列中，轉換成一個一維陣列。然後需要按照對角線 S 型的方式做排列順序。如範例一的圖示。

解法解析

這題官方給了兩種解法方式，基本概念還是主要計算 index 的方式。但是在討論區 tpt5cu 給出的解法，我覺得更簡單和好懂。

Diagonal Iteration and Reversal

這個解法是先從 row 行來遍歷(由左到右)，到底後再換成 column 列來遍歷(由上到下)。每次移動時再來走對角線，其中在判斷是否為複數行來判斷是否需要做反轉方向。

Time：O(N⋅M) Space：O(min(N, M))

Simulation

這個解法就滿麻煩的，是模擬對角線 S 型的方式來遍歷整個陣列。讓情況複雜許多，但是其空間複雜度是最低的，只有 O(1)

Time：O(N⋅M) Space：O(1)

From discuss

這個解法就是從討論區來的，其概念很簡單，在同一個對角線的元素，其索引的相加都是相同的。例如 matrix[1][0] 和 matrix[0][1]，的是在同一個對角線上，而且索引相加都是 1。所以很間單的對其相加的欄位放在一起，最後再依照複數行來判斷是否需要做反轉方向。

Time：O(N⋅M) Space：O(N + M)

解法範例

Go

Diagonal Iteration and Reversal

func findDiagonalOrder(mat [][]int) []int {
    var (
        N            int = len(mat)
        M            int = len(mat[0])
        result       []int
        intermediate []int
    )

    for d := 0; d < N+M-1; d++ {
        intermediate = []int{}
        var r, c int

        if d < M {
            r, c = 0, d
        } else {
            r, c = d-M+1, M-1
        }

        for r < N && c >= 0 {
            intermediate = append(intermediate, mat[r][c])
            r++
            c--
        }

        if d%2 == 0 {
            for j := len(intermediate) - 1; j >= 0; j-- {
                result = append(result, intermediate[j])
            }
        } else {
            result = append(result, intermediate...)
        }
    }

    return result
}

Simulation

func findDiagonalOrder(mat [][]int) []int {
    var (
        N         int = len(mat)
        M         int = len(mat[0])
        row       int = 0
        column    int = 0
        direction int = 1
        result    []int
    )

    for row < N && column < M {
        result = append(result, mat[row][column])
        var newRow, newColumn int
        if direction == 1 {
            newRow = row - 1
            newColumn = column + 1
        } else {
            newRow = row + 1
            newColumn = column - 1
        }

        if newRow < 0 || newRow >= N || newColumn < 0 || newColumn >= M {
            if direction > 0 {
                if column == M-1 {
                    row += 1
                }
                if column < M-1 {
                    column += 1
                }
            } else {
                if row == N-1 {
                    column += 1
                }
                if row < N-1 {
                    row += 1
                }
            }

            direction = 1 - direction
        } else {
            row = newRow
            column = newColumn
        }
    }

    return result
}

From discuss

func findDiagonalOrder(mat [][]int) []int {
    d := [][]int{}
    for i := 0; i < len(mat); i++ {
        for j := 0; j < len(mat[i]); j++ {
            if i+j < len(d) {
                d[i+j] = append(d[i+j], mat[i][j])
            } else {
                d = append(d, []int{mat[i][j]})
            }
        }
    }

    result := []int{}
    for idx, values := range d {
        if idx%2 == 0 {
            for j := len(values) - 1; j >= 0; j-- {
                result = append(result, values[j])
            }
        } else {
            result = append(result, values...)
        }
    }
    return result
}

JavaScript

Diagonal Iteration and Reversal

/**
 * @param {number[][]} mat
 * @return {number[]}
 */
var findDiagonalOrder = function (mat) {
    if (!mat || mat.length === 0) {
        return [];
    }
    const N = mat.length,
        M = mat[0].length,
        result = [];
    let intermediate = [];

    for (let d = 0; d < N + M - 1; d++) {
        intermediate = [];
        let r = d - M + 1;
        let c = M - 1;
        if (d < M) {
            r = 0;
            c = d;
        }

        while (r < N && c >= 0) {
            intermediate.push(mat[r][c]);
            r++;
            c--;
        }

        if (d % 2 === 0) {
            intermediate = intermediate.reverse();
        }
        result.push(...intermediate);
    }

    return result;
};

Simulation

/**
 * @param {number[][]} mat
 * @return {number[]}
 */
var findDiagonalOrder = function (mat) {
    if (!mat || mat.length === 0) {
        return [];
    }

    const N = mat.length,
        M = mat[0].length,
        result = [];
    let row = 0,
        column = 0,
        direction = 1;

    while (row < N && column < M) {
        result.push(mat[row][column]);

        let newRow = row + (direction === 1 ? -1 : 1);
        let newColumn = column + (direction === 1 ? 1 : -1);

        if (newRow < 0 || newRow === N || newColumn < 0 || newColumn === M) {
            if (direction) {
                row += column === M - 1 ? 1 : 0;
                column += column < M - 1 ? 1 : 0;
            } else {
                column += row === N - 1 ? 1 : 0;
                row += row < N - 1 ? 1 : 0;
            }

            direction = 1 - direction;
        } else {
            row = newRow;
            column = newColumn;
        }
    }

    return result;
};

From discuss

/**
 * @param {number[][]} mat
 * @return {number[]}
 */
var findDiagonalOrder = function (mat) {
    const d = {};

    for (let i = 0; i < mat.length; i++) {
        for (let j = 0; j < mat[0].length; j++) {
            d[i + j] = d[i + j] || [];
            d[i + j].push(mat[i][j]);
        }
    }

    const result = [];
    for (const key in d) {
        if (key % 2 === 0) {
            result.push(...d[key].reverse());
        } else {
            result.push(...d[key]);
        }
    }

    return result;
};

Kotlin

PHP

Diagonal Iteration and Reversal

class Solution
{

    /**
     * @param Integer[][] $mat
     * @return Integer[]
     */
    function findDiagonalOrder($mat)
    {
        $N = count($mat);
        $M = count($mat[0]);
        $result = array();
        $intermediate = array();

        for ($d = 0; $d < $N + $M - 1; $d++) {
            $intermediate = array();

            if ($d < $M) {
                $r = 0;
                $c = $d;
            } else {
                $r = $d - $M + 1;
                $c = $M - 1;
            }

            while ($r < $N && $c >= 0) {
                $intermediate[] = $mat[$r][$c];
                $r++;
                $c--;
            }

            if ($d % 2 == 0) {
                $result = array_merge($result, array_reverse($intermediate));
            } else {
                $result = array_merge($result, $intermediate);
            }
        }

        return $result;
    }
}

Simulation

class Solution
{

    /**
     * @param Integer[][] $mat
     * @return Integer[]
     */
    function findDiagonalOrder($mat)
    {
        $m = count($mat);
        $n = count($mat[0]);

        $r = $c = 0;

        for ($i = 0; $i < $m * $n; $i++) {
            $ans[] = $mat[$r][$c];

            if (($r + $c) % 2 == 0) {
                if ($c == $n - 1) {
                    $r++;
                } elseif ($r == 0) {
                    $c++;
                } else {
                    $r--;
                    $c++;
                }
            } else {
                if ($r == $m - 1) {
                    $c++;
                } elseif ($c == 0) {
                    $r++;
                } else {
                    $r++;
                    $c--;
                }
            }
        }

        return $ans;
    }
}

From discuss

class Solution
{

    /**
     * @param Integer[][] $mat
     * @return Integer[]
     */
    function findDiagonalOrder($mat)
    {
        $d = array();
        for ($i = 0; $i < count($mat); $i++) {
            for ($j = 0; $j < count($mat[$i]); $j++) {
                if (!isset($d[$i + $j])) {
                    $d[$i + $j] = array();
                }
                $d[$i + $j][] = $mat[$i][$j];
            }
        }

        $result = array();
        foreach ($d as $key => $value) {
            if ($key % 2 == 0) {
                $result = array_merge($result, array_reverse($value));
            } else {
                $result = array_merge($result, $value);
            }
        }

        return $result;
    }
}

Python

Diagonal Iteration and Reversal

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        # Check for empty matrices
        if not mat or not mat[0]:
            return []

        # Variables to track the size of the matrix
        N, M = len(mat), len(mat[0])

        # The two arrays as explained in the algorithm
        result, intermediate = [], []

        # We have to go over all the elements in the first
        # row and the last column to cover all possible diagonals
        for d in range(N + M - 1):

            # Clear the intermediate array everytime we start
            # to process another diagonal
            intermediate.clear()

            # We need to figure out the "head" of this diagonal
            # The elements in the first row and the last column
            # are the respective heads.
            if d < M:
                r, c = 0, d
            else:
                r, c = d - M + 1, M - 1

            # Iterate until one of the indices goes out of scope
            # Take note of the index math to go down the diagonal
            while r < N and c > -1:
                intermediate.append(mat[r][c])
                r += 1
                c -= 1

            # Reverse even numbered diagonals. The
            # article says we have to reverse odd
            # numbered articles but here, the numbering
            # is starting from 0 :P
            if d % 2 == 0:
                result.extend(intermediate[::-1])
            else:
                result.extend(intermediate)
        return result

Simulation

class Solution:

    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:

        # Check for an empty matrix
        if not mat or not mat[0]:
            return []

        # The dimensions of the matrix
        N, M = len(mat), len(mat[0])

        # Incides that will help us progress through
        # the matrix, one element at a time.
        row, column = 0, 0

        # As explained in the article, this is the variable
        # that helps us keep track of what direction we are
        # processing the current diaonal
        direction = 1

        # Final result array that will contain all the elements
        # of the matrix
        result = []

        # The uber while loop which will help us iterate over all
        # the elements in the array.
        while row < N and column < M:

            # First and foremost, add the current element to
            # the result matrix.
            result.append(mat[row][column])

            # Move along in the current diagonal depending upon
            # the current direction.[i, j] -> [i - 1, j + 1] if
            # going up and [i, j] -> [i + 1][j - 1] if going down.
            new_row = row + (-1 if direction == 1 else 1)
            new_column = column + (1 if direction == 1 else -1)

            # Checking if the next element in the diagonal is within the
            # bounds of the matrix or not. If it's not within the bounds,
            # we have to find the next head.
            if new_row < 0 or new_row == N or new_column < 0 or new_column == M:

                # If the current diagonal was going in the upwards
                # direction.
                if direction:

                    # For an upwards going diagonal having [i, j] as its tail
                    # If [i, j + 1] is within bounds, then it becomes
                    # the next head. Otherwise, the element directly below
                    # i.e. the element [i + 1, j] becomes the next head
                    row += (column == M - 1)
                    column += (column < M - 1)
                else:

                    # For a downwards going diagonal having [i, j] as its tail
                    # if [i + 1, j] is within bounds, then it becomes
                    # the next head. Otherwise, the element directly below
                    # i.e. the element [i, j + 1] becomes the next head
                    column += (row == N - 1)
                    row += (row < N - 1)

                # Flip the direction
                direction = 1 - direction
            else:
                row = new_row
                column = new_column

        return result

From discuss

class Solution(object):

    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        """
        :type mat: List[List[int]]
        :rtype: List[int]
        """
        d = {}
        # loop through matrix
        for i in range(len(mat)):
            for j in range(len(mat[i])):
                # if no entry in dictionary for sum of indices aka the diagonal, create one
                if i + j not in d:
                    d[i + j] = []
                # If you've already passed over this diagonal, keep adding elements to it!
                d[i + j].append(mat[i][j])

        # we're done with the pass, let's build our answer array
        ans = []
        # look at the diagonal and each diagonal's elements
        for entry in d.items():
            # each entry looks like (diagonal level (sum of indices), [elem1, elem2, elem3, ...])
            # snake time, look at the diagonal level
            if entry[0] % 2 == 0:
                # Here we append in reverse order because its an even numbered level/diagonal.
                ans.extend(entry[1][::-1])
            else:
                ans.extend(entry[1])
        return ans

Rust

Swift