538. Convert BST to Greater Tree

題目敘述

Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.

As a reminder, a binary search tree is a tree that satisfies these constraints:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

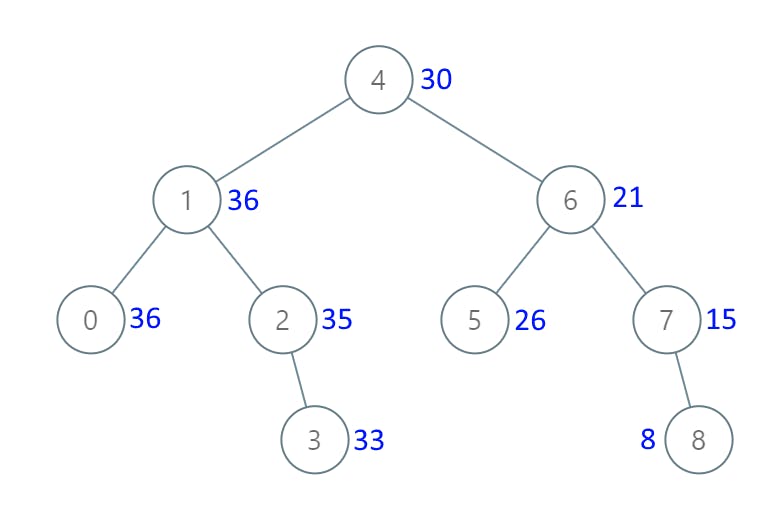
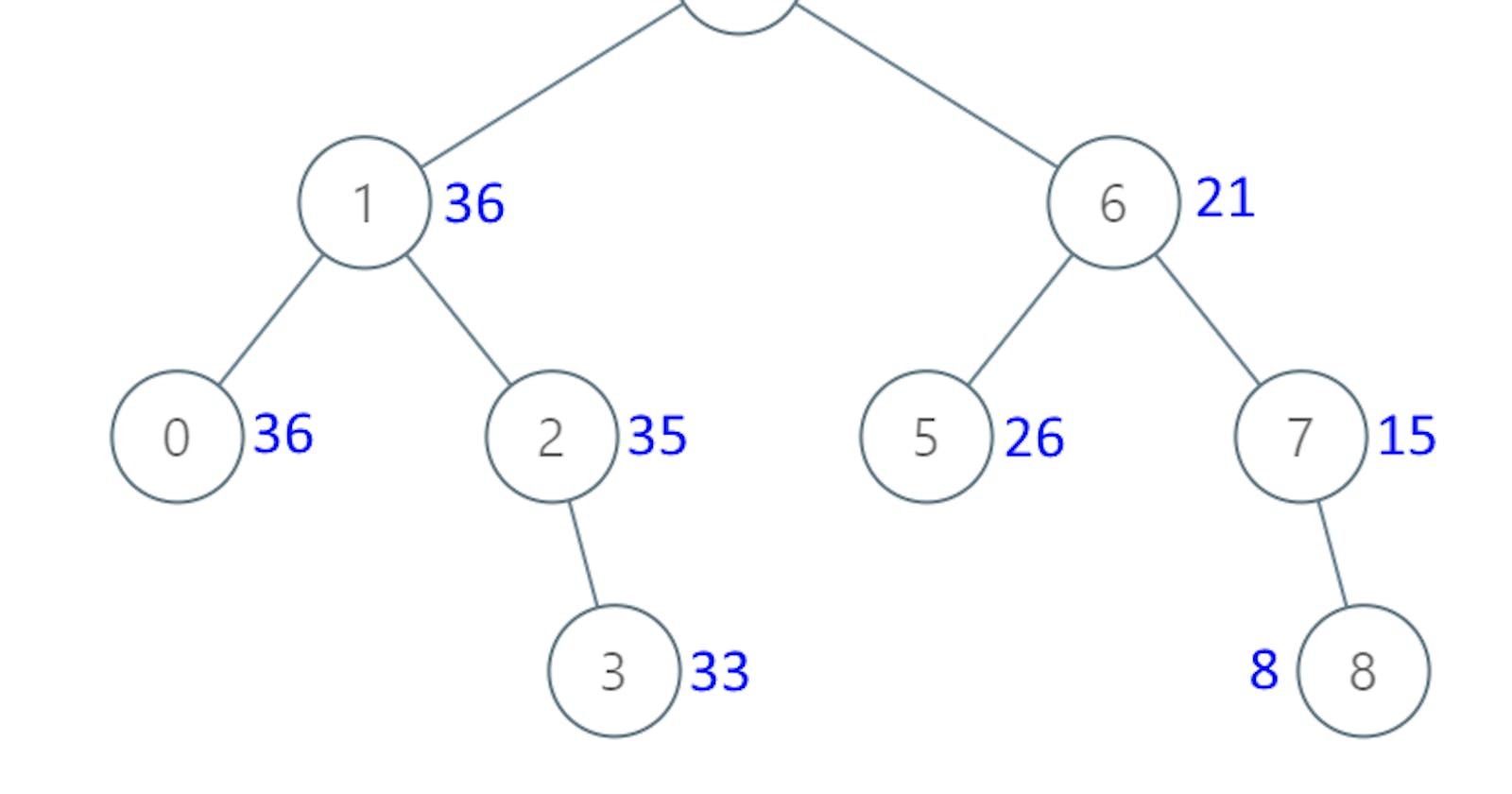
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

Input: root = [0,null,1]
Output: [1,null,1]

Constraints:

• The number of nodes in the tree is in the range [0, 10**4].
• 10**4 <= Node.val <= 10**4
• All the values in the tree are unique.
• root is guaranteed to be a valid binary search tree.

Note: This question is the same as 1038: https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/

題目翻譯

這題會給一個二元搜尋樹，然後要從大到小依序的累加。可以看範例一的圖，從 8 一路的累加到 0。

解法解析

這題的解法官方有三種，Recursion、Iteration with a Stack、Morris In-order Traversal。前面兩種時間複雜度跟空間複雜度都一樣是 O(n)。最後一個演算法，可以達到空間複雜度只有 O(1)。但我要吐槽一下，結果我每個程式解答送出後，都是前兩個在前面，有時候真的演算法看看就好，真的還是跑起來才知道呢。

Recursion

這是滿簡單的思維，就是我們用反序的方式遍歷整個二元搜尋樹，然後紀錄每一次的加總並更新節點的值。

Iteration with a Stack

有點算是從 Recursion 而來的想法，首先初始化一個空的 Stack 並把 root 作為當前節點。跟 Recursion 不同的是，我們是透過 Stack 來記住上一個節點。

Morris In-order Traversal

1. 當節點的右節點為空，代表沒有更大的值，所以處理加總當前節點後去遍歷左節點
2. 當節點的右節點不為空，代表還有更大的值。找出右節點的最左節點（因為會是當前排序的下一個節點）
   1. 當左節點的不存在，則將其指向當前節點( 代表說反序時，下一個值是目前的節點）
   2. 當左節點存在且跟當前節點不同（因為有可能是上面步驟增加的連結），則將其左節點社為空，並處理當前結點

解法範例

Go

Recursion

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func convertBST(root *TreeNode) *TreeNode {
    total := 0
    var convert func(*TreeNode)
    convert = func(node *TreeNode) {
        if node != nil {
            convert(node.Right)
            total += node.Val
            node.Val = total
            convert(node.Left)
        }
    }
    convert(root)
    return root
}

Iteration

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func convertBST(root *TreeNode) *TreeNode {
    total := 0
    node := root
    stack := make([]*TreeNode, 0)
    for node != nil || len(stack) > 0 {
        for node != nil {
            stack = append(stack, node)
            node = node.Right
        }

        node = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        total += node.Val
        node.Val = total
        node = node.Left
    }
    return root
}

Morris Traversal

func getSuccessor(node *TreeNode) *TreeNode {
    succ := node.Right
    for succ.Left != nil && succ.Left != node {
        succ = succ.Left
    }
    return succ
}

func convertBST(root *TreeNode) *TreeNode {
    total := 0
    node := root
    for node != nil {
        if node.Right == nil {
            total += node.Val
            node.Val = total
            node = node.Left
        } else {
            succ := getSuccessor(node)
            if succ.Left == nil {
                succ.Left = node
                node = node.Right
            } else {
                succ.Left = nil
                total += node.Val
                node.Val = total
                node = node.Left
            }
        }
    }
    return root
}

JavaScript

Recursion

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var convertBST = function (root) {
    let total = 0;
    convert(root);

    function convert(root) {
        if (!root) return;
        convert(root.right);
        total += root.val;
        root.val = total;
        convert(root.left);
    }
    return root;
};

Iteration

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var convertBST = function (root) {
    let total = 0,
        node = root;
    const stack = [];
    while (node || stack.length) {
        while (node) {
            stack.push(node);
            node = node.right;
        }

        node = stack.pop();
        total += node.val;
        node.val = total;
        node = node.left;
    }
    return root;
};

Morris Traversal

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var convertBST = function (root) {
    let total = 0,
        node = root;
    while (node) {
        if (!node.right) {
            total += node.val;
            node.val = total;
            node = node.left;
        } else {
            const succ = getSuccessor(node);
            if (succ.left) {
                succ.left = null;
                total += node.val;
                node.val = total;
                node = node.left;
            } else {
                succ.left = node;
                node = node.right;
            }
        }
    }

    return root;
};

const getSuccessor = (node) => {
    let succ = node.right;
    while (succ.left && succ.left !== node) {
        succ = succ.left;
    }
    return succ;
};

Kotlin

PHP

Python

Recursion

class Solution(object):
    def __init__(self):
        self.total = 0

    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if root is not None:
            self.convertBST(root.right)
            self.total += root.val
            root.val = self.total
            self.convertBST(root.left)
        return root

Iteration

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        total = 0

        node = root
        stack: List[TreeNode] = []
        while stack or node is not None:
            # push all nodes up to (and including) this subtree's maximum on
            # the stack.
            while node is not None:
                stack.append(node)
                node = node.right

            node = stack.pop()
            total += node.val
            node.val = total

            # all nodes with values between the current and its parent lie in
            # the left subtree.
            node = node.left

        return root

Morris Traversal

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # Get the node with the smallest value greater than this one.
        def get_successor(node):
            succ = node.right
            while succ.left is not None and succ.left is not node:
                succ = succ.left
            return succ

        total = 0
        node = root
        while node is not None:
            # If there is no right subtree, then we can visit this node and
            # continue traversing left.
            if node.right is None:
                total += node.val
                node.val = total
                node = node.left
            # If there is a right subtree, then there is a node that has a
            # greater value than the current one. therefore, we must traverse
            # that node first.
            else:
                succ = get_successor(node)
                # If there is no left subtree (or right subtree, because we are
                # in this branch of control flow), make a temporary connection
                # back to the current node.
                if succ.left is None:
                    succ.left = node
                    node = node.right
                # If there is a left subtree, it is a link that we created on
                # a previous pass, so we should unlink it and visit this node.
                else:
                    succ.left = None
                    total += node.val
                    node.val = total
                    node = node.left

        return root

Rust

Swift

Reference

• github.com/chen-zyc/leetcode/blob/master/do..
• zhuanlan.zhihu.com/p/257119723