54. Spiral Matrix

題目敘述

Given an m x n matrix, return all elements of the matrix in spiral order.

Example 1:

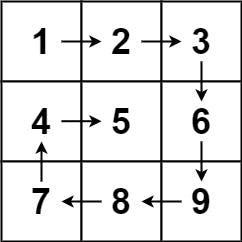
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

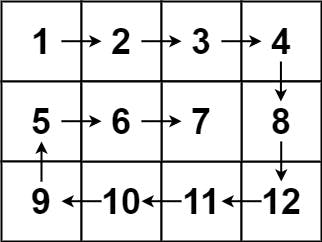
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

Hint 1:

Well for some problems, the best way really is to come up with some algorithms for simulation. Basically, you need to simulate what the problem asks us to do.

Hint 2:

We go boundary by boundary and move inwards. That is the essential operation. First row, last column, last row, first column and then we move inwards by 1 and then repeat. That's all, that is all the simulation that we need.

Hint 3:

Think about when you want to switch the progress on one of the indexes. If you progress on i out of [i, j], you'd be shifting in the same column. Similarly, by changing values for j, you'd be shifting in the same row. Also, keep track of the end of a boundary so that you can move inwards and then keep repeating. It's always best to run the simulation on edge cases like a single column or a single row to see if anything breaks or not.

題目翻譯

題目很簡單，會給一個 m x n 的 matrix 矩陣，然後依照螺旋順序回傳所有的元素

解法解析

這題的解法是用了設定了邊界的方式，慢慢的縮小。可以看到範例 Python 中就是先定義了，四個方向的初始值。依序的處理了，往右、往下、往左、往上，走完一圈後，將邊界縮小。重複此動作將全部元素走完。

解法範例

Go

func spiralOrder(matrix [][]int) []int {
    ordered := append([]int{}, matrix[0]...)
    m, n := len(matrix), len(matrix[0])
    total := m * n

    dir, pos, movement := 0, []int{0, n - 1}, [][]int{{1, 0}, {0, -1}, {-1, 0}, {0, 1}}
    for len(ordered) < total {
        for i := 1; i < m; i++ {
            pos[0] += movement[dir][0]
            pos[1] += movement[dir][1]

            ordered = append(ordered, matrix[pos[0]][pos[1]])
        }

        m--
        m, n = n, m

        dir = (dir + 1) % 4
    }

    return ordered

JavaScript

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
    const result = [];
    const rows = matrix.length, columns = matrix[0].length;
    let up = 0, left = 0;
    let right = columns - 1;
    let down = rows - 1;

    while (result.length < rows * columns) {
        for (let col = left; col <= right; col++) {
            result.push(matrix[up][col]);
        }

        for (let row = up + 1; row <= down; row++) {
            result.push(matrix[row][right]);
        }

        if (up !== down) {
            for (let col = right - 1;  left - 1 < col; col--) {
                result.push(matrix[down][col]);
            }
        }

        if (left !== right) {
            for (let row = down - 1; up < row; row--) {
                result.push(matrix[row][left]);
            }
        }

        left++;
        right--;
        up++;
        down--;
    }

    return result;
}

Kotlin

class Solution {
    fun spiralOrder(matrix: Array<IntArray>): List<Int> {
        val order = mutableListOf<Int>()
        if (matrix.isEmpty()) {
            return order
        }

        var startRow = 0
        var endRow = matrix.size - 1
        var startColumn = 0
        var endColumn = matrix[0].size - 1

        while (startRow <= endRow && startColumn <= endColumn) {
            // Right
            for (column in startColumn..endColumn) {
                order.add(matrix[startRow][column])
            }

            // Down
            for (row in startRow + 1..endRow) {
                order.add(matrix[row][endColumn])
            }

            // Left
            for (column in endColumn - 1 downTo startColumn) {
                if (startRow == endRow) break
                order.add(matrix[endRow][column])
            }

            // Up
            for (row in endRow - 1 downTo startRow + 1) {
                if (startColumn == endColumn) break
                order.add(matrix[row][startColumn])
            }

            startRow++
            endRow--
            startColumn++
            endColumn--
        }

        return order
    }
}

PHP

Python

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        result = []
        rows, columns = len(matrix), len(matrix[0])
        up = left = 0
        right = columns - 1
        down = rows - 1

        while len(result) < rows * columns:
            # Traverse from left to right.
            for col in range(left, right + 1):
                result.append(matrix[up][col])

            # Traverse downwards.
            for row in range(up + 1, down + 1):
                result.append(matrix[row][right])

            # Make sure we are now on a different row.
            if up != down:
                # Traverse from right to left.
                for col in range(right - 1, left - 1, -1):
                    result.append(matrix[down][col])

            # Make sure we are now on a different column.
            if left != right:
                # Traverse upwards.
                for row in range(down - 1, up, -1):
                    result.append(matrix[row][left])

            left += 1
            right -= 1
            up += 1
            down -= 1

        return result

Rust

Swift

class Solution {
    func spiralOrder(_ matrix: [[Int]]) -> [Int] {
        guard  !matrix.isEmpty else {
            return []
        }
        var top = 0
        var bottom = matrix.count - 1
        var left = 0
        var right = matrix[0].count - 1
        let count = matrix.count * matrix[0].count
        var arr = [Int]()
        while arr.count < count {

            for i in stride(from: left, to: right+1, by: 1) where arr.count < count {
                arr.append(matrix[top][i])
            }
            top += 1
            for i in stride(from: top, to: bottom+1, by: 1) where arr.count < count {
                arr.append(matrix[i][right])
            }
            right -= 1
            for i in stride(from: right, to: left-1, by: -1) where arr.count < count {
                arr.append(matrix[bottom][i])
            }
            bottom -= 1
            for i in stride(from: bottom, to: top-1, by: -1) where arr.count < count {
                arr.append(matrix[i][left])
            }
            left += 1
        }
        return arr
    }
}