59. Spiral Matrix II

題目敘述

Given a positive integer n, generate an n x n matrix filled with elements from 1 to n**2 in spiral order.

Example 1:

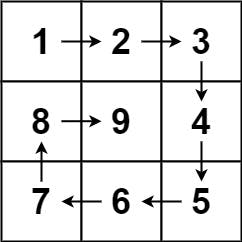
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

Example 2:

Input: n = 1
Output: [[1]]

Constraints:

• 1 <= n <= 20

題目翻譯

題目的需求很簡單就是會給一個整數參數 n，然後從數字 1 開始從外而內做順時針的螺旋排列。

解法解析

這題的解法有以下幾種方式：

1. 依照題目所說的從外而內的螺旋排列
2. 由內而外的排序，可以參考討論區的部分

其實主要就是判斷這個邊界索引的邏輯，有幾種方式：

1. 用四個變數紀錄四個方向的索引，如 Go 的第二個範例
2. 直接用計算的方式處理，優化的方式是使用取模。如 JavaScript 和 Python 的第二個範例

解法範例

Go

Traverse Layer

func generateMatrix(n int) [][]int {
    result := make([][]int, n)
    for i := range result {
        result[i] = make([]int, n)
    }
    var cnt int = 1
    for layer := 0; layer < (n+1)/2; layer++ {
        for i := layer; i < n-layer; i++ {
            result[layer][i] = cnt
            cnt++
        }
        for i := layer + 1; i < n-layer; i++ {
            result[i][n-layer-1] = cnt
            cnt++
        }
        for i := n - layer - 2; i >= layer; i-- {
            result[n-layer-1][i] = cnt
            cnt++
        }
        for i := n - layer - 2; i > layer; i-- {
            result[i][layer] = cnt
            cnt++
        }
    }
    return result
}

Traverse Layer for 4 directino

func generateMatrix(n int) [][]int {
    if n == 0 {
        return [][]int{}
    }

    result := make([][]int, n)
    for i := range result {
        result[i] = make([]int, n)
    }

    var top, bottom, left, right int = 0, n - 1, 0, n - 1
    var cnt, layerRange int = 1, n * n
    for cnt <= layerRange {
        for i := left; i <= right && cnt <= layerRange; i++ {
            result[top][i] = cnt
            cnt++
        }
        top++

        for i := top; i <= bottom && cnt <= layerRange; i++ {
            result[i][right] = cnt
            cnt++
        }
        right--

        for i := right; i >= left && cnt <= layerRange; i-- {
            result[bottom][i] = cnt
            cnt++
        }
        bottom--

        for i := bottom; i >= top && cnt <= layerRange; i-- {
            result[i][left] = cnt
            cnt++
        }
        left++
    }

    return result
}

JavaScript

Traverse Layer

/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function (n) {
    const result = new Array(n).fill(0).map(() => new Array(n).fill(0));
    let cnt = 1;
    for (let layer = 0; layer < Math.floor((n + 1) / 2); layer++) {
        for (let i = layer; i < n - layer; i++) {
            result[layer][i] = cnt++;
        }
        for (let i = layer + 1; i < n - layer; i++) {
            result[i][n - layer - 1] = cnt++;
        }
        for (let i = layer + 1; i < n - layer; i++) {
            result[n - layer - 1][n - i - 1] = cnt++;
        }
        for (let i = layer + 1; i < n - layer - 1; i++) {
            result[n - i - 1][layer] = cnt++;
        }
    }

    return result;
};

Optimized spiral traversal

/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function (n) {
    const result = [...Array(n)].map(() => Array(n).fill(0));
    const dir = [
        [0, 1],
        [1, 0],
        [0, -1],
        [-1, 0],
    ];

    let row = 0,
        col = 0,
        d = 0,
        cnt = 1;
    while (cnt <= n * n) {
        result[row][col] = cnt++;

        let r = (row + dir[d][0]) % n;
        let c = (col + dir[d][1]) % n;

        if (result[r][c] !== 0) {
            d = (d + 1) % 4;
        }

        row += dir[d][0];
        col += dir[d][1];
    }

    return result;
};

Kotlin

PHP

Python

Traverse Layer

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        result = [[0 for _ in range(n)] for _ in range(n)]
        cnt = 1
        for layer in range((n + 1) // 2):
            # direction 1 - traverse from left to right
            for i in range(layer, n - layer):
                result[layer][i] = cnt
                cnt += 1
            # direction 2 - traverse from top to bottom
            for i in range(layer + 1, n - layer):
                result[i][n - layer - 1] = cnt
                cnt += 1
            # direction 3 - traverse from right to left
            for i in range(layer + 1, n - layer):
                result[n - layer - 1][n - i - 1] = cnt
                cnt += 1
            # direction 4 - traverse from bottom to top
            for i in range(layer + 1, n - layer - 1):
                result[n - i - 1][layer] = cnt
                cnt += 1
        return result

Optimized spiral traversal

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        result = [[0 for _ in range(n)] for _ in range(n)]
        # right, down, left, up
        dr = [[0, 1], [1, 0], [0, -1], [-1, 0]]
        row, col, d, cnt = 0, 0, 0, 1

        while cnt <= n * n:
            result[row][col] = cnt

            r = (row + dr[d][0]) % n
            c = (col + dr[d][1]) % n

            if result[r][c] != 0:
                d = (d + 1) % 4

            row += dr[d][0]
            col += dr[d][1]
            cnt += 1

        return result

Rust

Swift