669. Trim a Binary Search Tree

題目敘述

Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

Example 1:

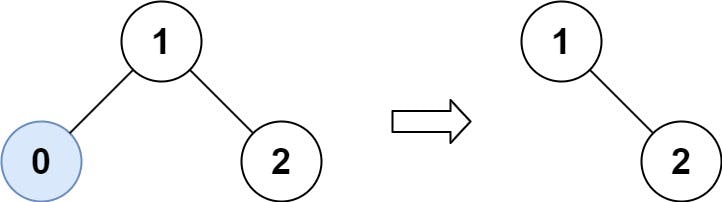
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]

Example 2:

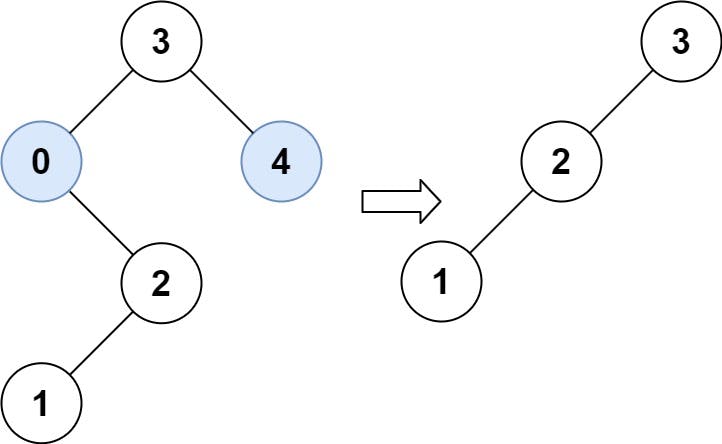
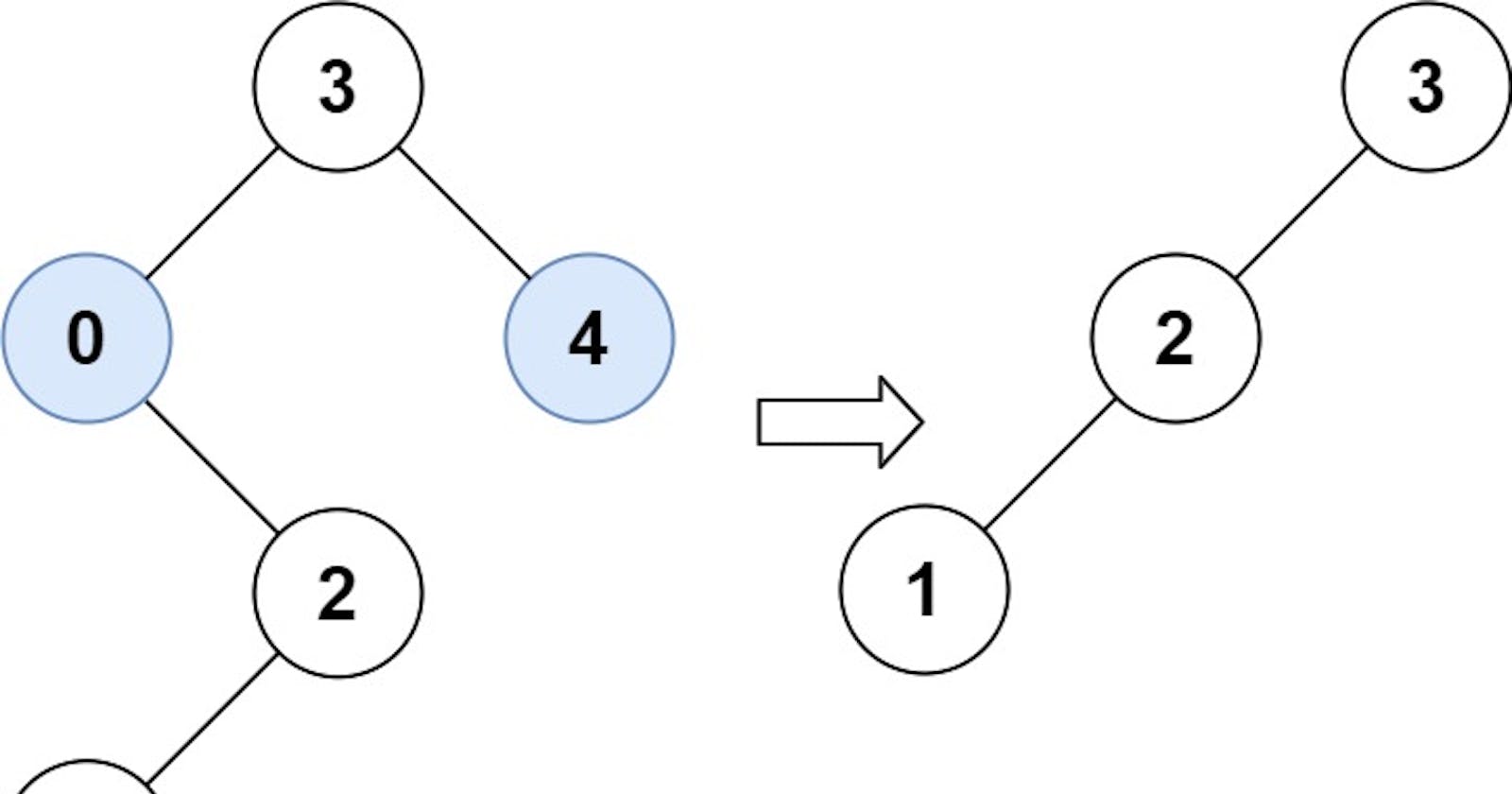
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]

Constraints:

• The number of nodes in the tree in the range [1, 104].
• 0 <= Node.val <= 10**4
• The value of each node in the tree is unique.
• root is guaranteed to be a valid binary search tree.
• 0 <= low <= high <= 10**4

題目翻譯

題目的需求很簡單，就是有一個二元搜尋樹 root。然後我們需要去修剪其中的節點，修剪的條件會有兩個參數 low 和 high，只要節點的值不在這個範圍內就會被刪減掉。

解法解析

這題的解法就是使用了遞迴，去搜尋全部的節點。對每個節點判斷其範圍後去覆蓋前一個節點的位置。

解法範例

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func trimBST(root *TreeNode, low int, high int) *TreeNode {
    if root == nil {
        return nil
    } else if root.Val < low {
        return trimBST(root.Right, low, high)
    } else if root.Val > high {
        return trimBST(root.Left, low, high)
    }
    root.Left = trimBST(root.Left, low, high)
    root.Right = trimBST(root.Right, low, high)
    return root
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} low
 * @param {number} high
 * @return {TreeNode}
 */
var trimBST = function (root, low, high) {
    if (!root) return null;
    if (root.val < low) return trimBST(root.right, low, high);
    if (root.val > high) return trimBST(root.left, low, high);
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    return root;
};

Kotlin

這邊是利用 Kotlin 可以將判斷式當作一個 return 的方式

/**
 * Example:
 * var ti = TreeNode(5)
 * var v = ti.`val`
 * Definition for a binary tree node.
 * class TreeNode(var `val`: Int) {
 *     var left: TreeNode? = null
 *     var right: TreeNode? = null
 * }
 */
class Solution {
    fun trimBST(root: TreeNode?, low: Int, high: Int): TreeNode? {
        return if (root == null) {
            null
        } else if (root.`val` < low) {
            trimBST(root.right, low, high)
        } else if (root.`val` > high) {
            trimBST(root.left, low, high)
        } else {
            root.left = trimBST(root.left, low, high)
            root.right = trimBST(root.right, low, high)
            root
        }
    }
}

PHP

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     public $val = null;
 *     public $left = null;
 *     public $right = null;
 *     function __construct($val = 0, $left = null, $right = null) {
 *         $this->val = $val;
 *         $this->left = $left;
 *         $this->right = $right;
 *     }
 * }
 */
class Solution
{

    /**
     * @param TreeNode $root
     * @param Integer $low
     * @param Integer $high
     * @return TreeNode
     */
    function trimBST($root, $low, $high)
    {
        if ($root == null) {
            return null;
        }
        if ($root->val < $low) {
            return $this->trimBST($root->right, $low, $high);
        }
        if ($root->val > $high) {
            return $this->trimBST($root->left, $low, $high);
        }
        $root->left = $this->trimBST($root->left, $low, $high);
        $root->right = $this->trimBST($root->right, $low, $high);
        return $root;
    }
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
        def trim(node):
            if node is None:
                return node
            elif node.val > high:
                return trim(node.left)
            elif node.val < low:
                return trim(node.right)
            else:
                node.left = trim(node.left)
                node.right = trim(node.right)
                return node

        return trim(root)

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn trim_bst(root: Option<Rc<RefCell<TreeNode>>>, low: i32, high: i32) -> Option<Rc<RefCell<TreeNode>>> {
        if let Some(node_ref) = root {
            let mut node = node_ref.borrow_mut();
            if node.val > high {
                return Self::trim_bst(node.left.clone(), low, high);
            } else if node.val < low {
                return Self::trim_bst(node.right.clone(), low, high);
            }
            node.left = Self::trim_bst(node.left.clone(), low, high);
            node.right = Self::trim_bst(node.right.clone(), low, high);
            Some(node_ref.clone())
        } else {
            None
        }
    }
}

Swift

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public var val: Int
 *     public var left: TreeNode?
 *     public var right: TreeNode?
 *     public init() { self.val = 0; self.left = nil; self.right = nil; }
 *     public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }
 *     public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {
 *         self.val = val
 *         self.left = left
 *         self.right = right
 *     }
 * }
 */
class Solution {
    func trimBST(_ root: TreeNode?, _ low: Int, _ high: Int) -> TreeNode? {
        guard let root = root else {
            return nil
        }
        if root.val < low {
            return trimBST(root.right, low, high)
        }
        if root.val > high {
            return trimBST(root.left, low, high)
        }
        root.left = trimBST(root.left, low, high)
        root.right = trimBST(root.right, low, high)
        return root
    }
}