74. Search a 2D Matrix

題目敘述

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

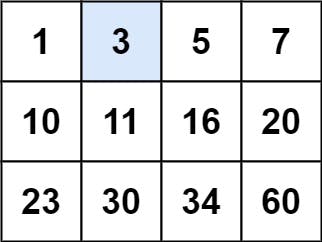
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 Output: true

Example 2:

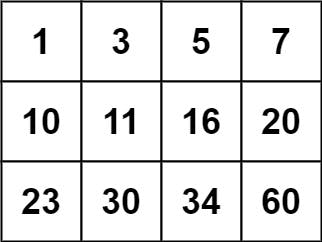
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10**4 <= matrix[i][j], target <= 10**4

題目翻譯

今天有一個 m x n 的二維矩陣，和一個 target 的參數。其中 matrix 的值是由小到大排序，當第一列排完後接續第二列。然後要在這個二維矩陣中找出是否包含 target 的值。

解法解析

我一開始的解題思路是，先跟每一列的第一個元素是做比較，查出說是在哪一列，第二步在針對那一列作搜尋。不過看了其他人的解題思路，才發現自己第一步多餘了，其實二維矩陣就是一個大的排序過的陣列，所以直接對其做 Binary Search 即可，唯一要處理的是怎麼從 index 轉換成行列的位置。

解法範例

Go

func searchMatrix(matrix [][]int, target int) bool {
    m := len(matrix)
    if m == 0 {
        return false
    }
    n := len(matrix[0])

    for left, right := 0, m*n-1; left <= right; {
        pivotIdx := (left + right) / 2
        pivotElement := matrix[pivotIdx/n][pivotIdx%n]
        if pivotElement == target {
            return true
        } else if target < pivotElement {
            right = pivotIdx - 1
        } else {
            left = pivotIdx + 1
        }
    }
    return false
}

JavaScript

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function (matrix, target) {
    const m = matrix.length;
    if (m === 0) return false;
    const n = matrix[0].length;

    for (let left = 0, right = m * n - 1; left <= right; ) {
        const pivotIdx = Math.floor((left + right) / 2);
        const pivotElement = matrix[Math.floor(pivotIdx / n)][pivotIdx % n];
        if (pivotElement === target) return true;
        if (target < pivotElement) right = pivotIdx - 1;
        else left = pivotIdx + 1;
    }
    return false;
};

Kotlin

class Solution {
    fun searchMatrix(matrix: Array<IntArray>, target: Int): Boolean {
        if (matrix.isEmpty()) return false
        val m = matrix.size
        val n = matrix[0].size
        var left = 0
        var right = m * n - 1
        while (left <= right) {
            val pivotIdx = (right + left) / 2
            val pivotElement = matrix[pivotIdx / n][pivotIdx % n]
            if (pivotElement == target) {
                return true
            } else if (pivotElement < target) {
                left = pivotIdx + 1
            } else {
                right = pivotIdx - 1
            }
        }
    }
}

PHP

class Solution
{
    /**
     * @param Integer[][] $matrix
     * @param Integer $target
     * @return Boolean
     */
    function searchMatrix($matrix, $target)
    {
        $m = count($matrix);
        if ($m == 0) {
            return false;
        }
        $n = count($matrix[0]);

        $left = 0;
        $right = $m * $n - 1;
        while ($left <= $right) {
            $pivotIdx = (int)(($left + $right) / 2);
            $pivotElement = $matrix[(int)($pivotIdx / $n)][$pivotIdx % $n];
            if ($pivotElement == $target) {
                return true;
            } else if ($pivotElement < $target) {
                $left = $pivotIdx + 1;
            } else {
                $right = $pivotIdx - 1;
            }
        }
        return false;
    }
}

Python

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m = len(matrix)
        if m == 0:
            return False
        n = len(matrix[0])

        # binary search
        left, right = 0, m * n - 1
        while left <= right:
            pivot_idx = (left + right) // 2
            pivot_element = matrix[pivot_idx // n][pivot_idx % n]
            if target == pivot_element:
                return True
            elif target < pivot_element:
                right = pivot_idx - 1
            else:
                left = pivot_idx + 1
        return False

Rust

impl Solution {
    pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {
        if matrix.is_empty() {
            return false;
        }
        let m = matrix.len();
        let n = matrix[0].len();

        let (mut left, mut right) = (0, m * n);
        while left < right {
            let pivot_idx = (left + right) / 2;
            let pivot_element = matrix[pivot_idx / n][pivot_idx % n];

            if target == pivot_element {
                return true;
            } else if target < pivot_element {
                right = pivot_idx;
            } else {
                left = pivot_idx + 1;
            }
        }

        false
    }
}

Swift

class Solution {
    func searchMatrix(_ matrix: [[Int]], _ target: Int) -> Bool {
        let m = matrix.count
        guard m > 0 else { return false }
        let n = matrix[0].count

        var left = 0, right = m * n - 1
        while left <= right {
            let pivotIdx = (left + right) / 2
            let pivotElement = matrix[pivotIdx / n][pivotIdx % n]
            if pivotElement == target {
                return true
            } else if target < pivotElement {
                right = pivotIdx - 1
            } else {
                left = pivotIdx + 1
            }
        }
        return false
    }
}