897. Increasing Order Search Tree
題目敘述
Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
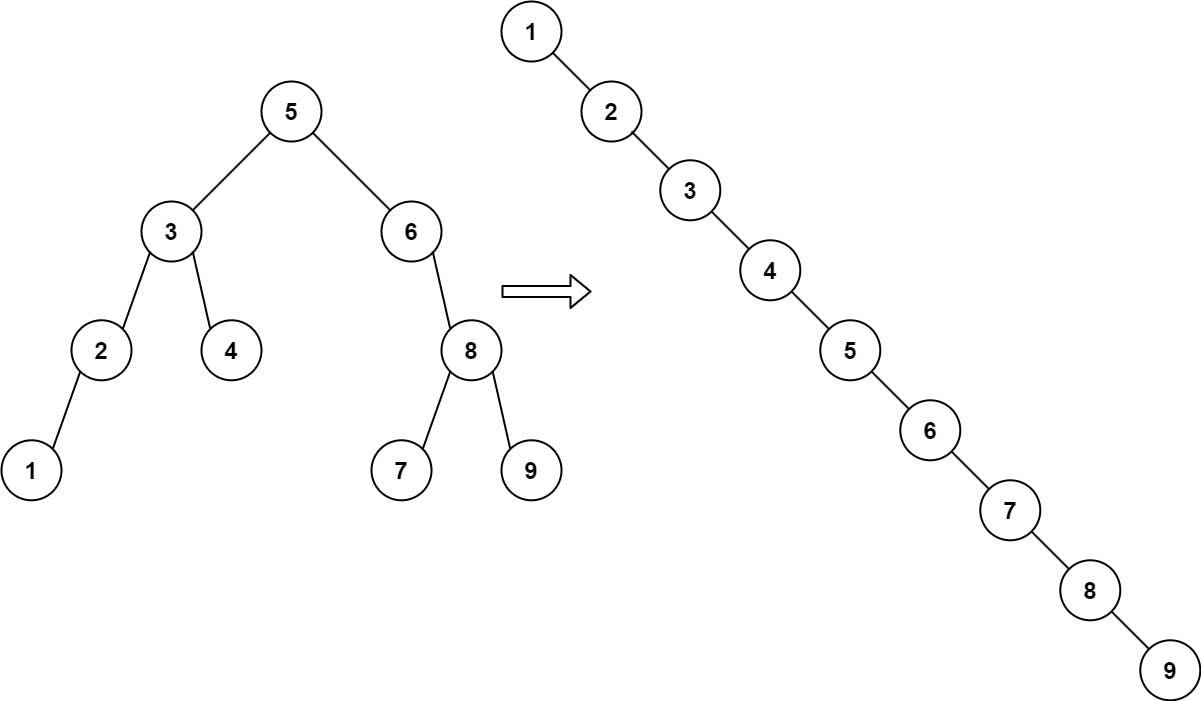
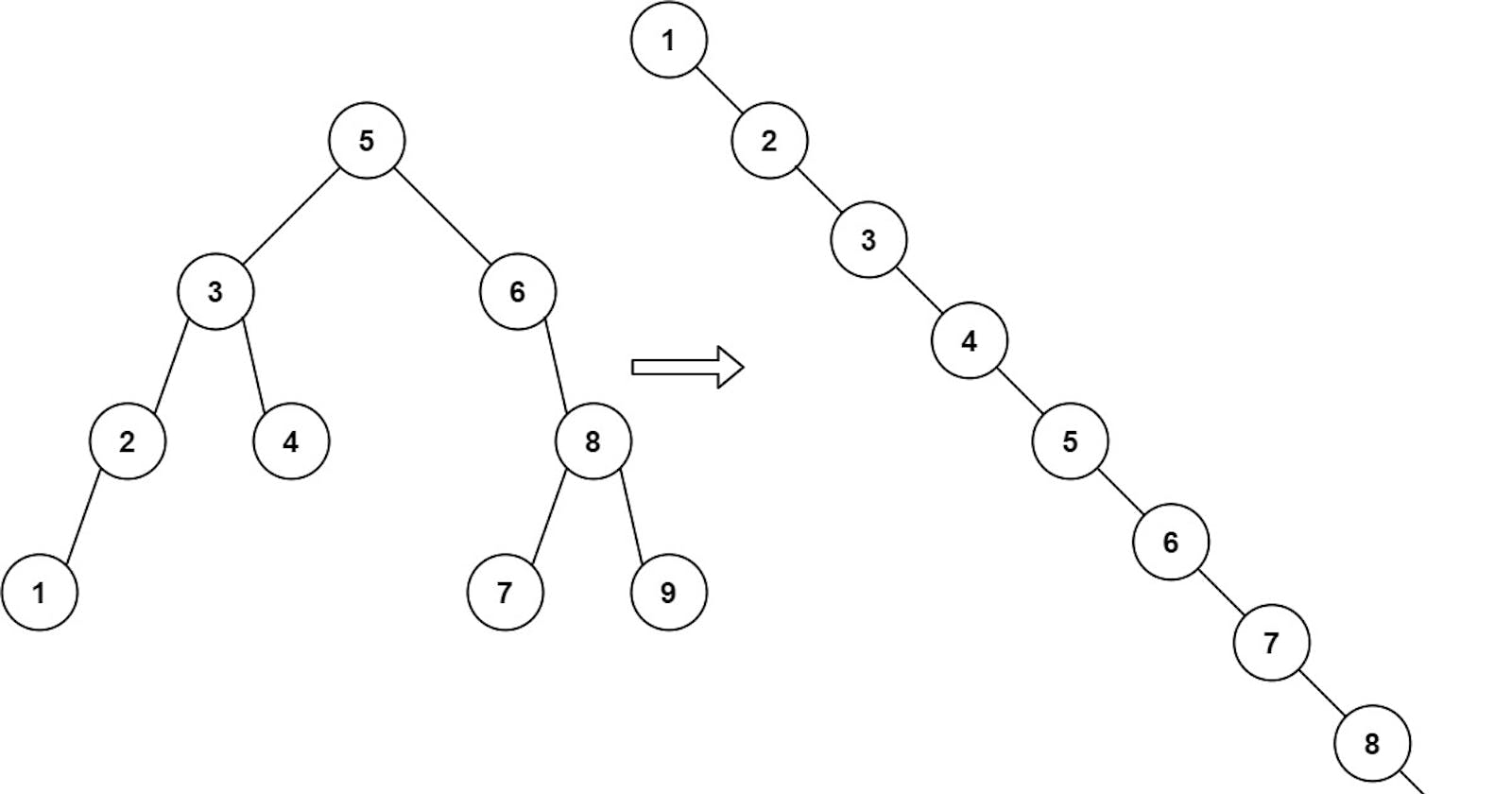
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
Example 2:
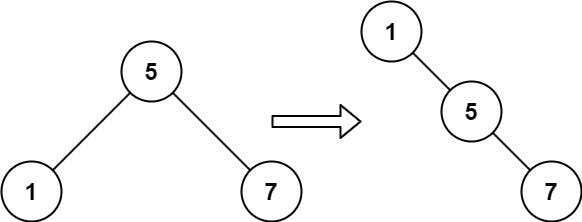
Input: root = [5,1,7]
Output: [1,null,5,null,7]
Constraints:
- The number of nodes in the given tree will be in the range
[1, 100]. 0 <= Node.val <= 1000
題目翻譯
這題目要將一個二元樹 root 轉換成由小到大排序的右側樹(所有節點都在右側)。如範例上的圖表示的結構。
解法解析
這題主要是利用二元樹的特性,所以其實遍歷每個節點的時候,只要將其依照 左節點 -> 當前節點 -> 右節點順序來存取,就可以排出由小到大的排序。剩下不同的就只是怎麼轉換結構,常見的方式有:重新連結、使用 Array 儲存順序等。
解法範例
Go
In-Order Traversal
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func increasingBST(root *TreeNode) *TreeNode {
vals := make([]int, 0)
inorder(root, &vals)
ans := &TreeNode{}
cur := ans
for _, v := range vals {
cur.Right = &TreeNode{Val: v}
cur = cur.Right
}
return ans.Right
}
func inorder(root *TreeNode, vals *[]int) {
if root == nil {
return
}
inorder(root.Left, vals)
*vals = append(*vals, root.Val)
inorder(root.Right, vals)
}
Traversal with Relinking
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func increasingBST(root *TreeNode) *TreeNode {
ans := &TreeNode{}
cur := ans
var inorder func(*TreeNode)
inorder = func(node *TreeNode) {
if node == nil {
return
}
inorder(node.Left)
node.Left = nil
cur.Right = node
cur = node
inorder(node.Right)
}
inorder(root)
return ans.Right
}
JavaScript
In-Order Traversal
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var increasingBST = function (root) {
const vals = [];
inorder(root, vals);
const ans = new TreeNode();
let cur = ans;
for (const v of vals) {
cur.right = new TreeNode(v);
cur = cur.right;
}
return ans.right;
};
const inorder = (node, vals) => {
if (node === null) return;
inorder(node.left, vals);
vals.push(node.val);
inorder(node.right, vals);
};
Traversal with Relinking
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var increasingBST = function (root) {
const ans = new TreeNode();
let cur = ans;
const inorder = (node) => {
if (!node) return;
inorder(node.left);
node.left = null;
cur.right = node;
cur = cur.right;
inorder(node.right);
};
inorder(root);
return ans.right;
};
Kotlin
In-Order Traversal
/**
* Example:
* var ti = TreeNode(5)
* var v = ti.`val`
* Definition for a binary tree node.
* class TreeNode(var `val`: Int) {
* var left: TreeNode? = null
* var right: TreeNode? = null
* }
*/
class Solution {
fun increasingBST(node: TreeNode?): TreeNode? {
val vals = mutableListOf<Int>()
inorder(node, vals)
val ans = TreeNode(0)
var cur = ans
for (v in vals) {
cur.right = TreeNode(v)
cur = cur.right
}
return ans.right
}
private fun inorder(node: TreeNode?, vals: MutableList<Int>) {
if (node == null) return
inorder(node.left, vals)
vals.add(node.`val`)
inorder(node.right, vals)
}
}
Traversal with Relinking
/**
* Example:
* var ti = TreeNode(5)
* var v = ti.`val`
* Definition for a binary tree node.
* class TreeNode(var `val`: Int) {
* var left: TreeNode? = null
* var right: TreeNode? = null
* }
*/
class Solution {
private var cur: TreeNode = TreeNode(0)
fun increasingBST(root: TreeNode?): TreeNode? {
var ans: TreeNode = cur
inorder(root)
return ans.right
}
fun inorder(node: TreeNode?) {
if (node == null) {
return
}
inorder(node.left)
node.left = null
cur.right = node
cur = cur.right
inorder(node.right)
}
}
PHP
In-Order Traversal
/**
* Definition for a binary tree node.
* class TreeNode {
* public $val = null;
* public $left = null;
* public $right = null;
* function __construct($val = 0, $left = null, $right = null) {
* $this->val = $val;
* $this->left = $left;
* $this->right = $right;
* }
* }
*/
class Solution
{
private $vals = [];
/**
* @param TreeNode $root
* @return TreeNode
*/
function increasingBST($root)
{
$this->inorder($root);
sort($this->vals);
$ans = new TreeNode(0);
$cur = $ans;
foreach ($this->vals as $v) {
$cur->right = new TreeNode($v);
$cur = $cur->right;
}
return $ans->right;
}
function inorder($node)
{
if ($node == null) {
return null;
}
$node->left = $this->inorder($node->left);
$this->vals[] = $node->val;
$node->right = $this->inorder($node->right);
}
}
Traversal with Relinking
/**
* Definition for a binary tree node.
* class TreeNode {
* public $val = null;
* public $left = null;
* public $right = null;
* function __construct($val = 0, $left = null, $right = null) {
* $this->val = $val;
* $this->left = $left;
* $this->right = $right;
* }
* }
*/
class Solution
{
/**
* @param TreeNode $root
* @return TreeNode
*/
function increasingBST($root)
{
$ans = new TreeNode(0);
$this->cur = $ans;
$this->inorder($root);
return $ans->right;
}
function inorder($node)
{
if ($node == null) {
return null;
}
$this->inorder($node->left);
$node->left = null;
$this->cur->right = $node;
$this->cur = $node;
$this->inorder($node->right);
}
}
Python
In-Order Traversal
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def increasingBST(self, root: TreeNode) -> TreeNode:
def inorder(node):
if node:
yield from inorder(node.left)
yield node.val
yield from inorder(node.right)
ans = cur = TreeNode(None)
for v in inorder(root):
cur.right = TreeNode(v)
cur = cur.right
return ans.right
Traversal with Relinking
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def increasingBST(self, root: TreeNode) -> TreeNode:
def inorder(node):
if node:
inorder(node.left)
node.left = None
self.cur.right = node
self.cur = node
inorder(node.right)
ans = self.cur = TreeNode(None)
inorder(root)
return ans.right
Rust
In-Order Traversal
Traversal with Relinking
Swift
In-Order Traversal
/**
* Definition for a binary tree node.
* public class TreeNode {
* public var val: Int
* public var left: TreeNode?
* public var right: TreeNode?
* public init() { self.val = 0; self.left = nil; self.right = nil; }
* public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }
* public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {
* self.val = val
* self.left = left
* self.right = right
* }
* }
*/
class Solution {
func increasingBST(_ root: TreeNode?) -> TreeNode? {
var vals: [Int] = []
inorder(root, &vals)
var ans = TreeNode(0)
var cur: TreeNode? = ans
for v in vals {
cur?.right = TreeNode(v)
cur = cur?.right
}
return ans.right
}
func inorder (_ node: TreeNode?, _ vals: inout [Int]) {
guard let node = node else { return }
inorder(node.left, &vals)
vals.append(node.val)
inorder(node.right, &vals)
}
}
Traversal with Relinking
/**
* Definition for a binary tree node.
* public class TreeNode {
* public var val: Int
* public var left: TreeNode?
* public var right: TreeNode?
* public init() { self.val = 0; self.left = nil; self.right = nil; }
* public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }
* public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {
* self.val = val
* self.left = left
* self.right = right
* }
* }
*/
class Solution {
var cur: TreeNode?
func increasingBST(_ root: TreeNode?) -> TreeNode? {
var ans = TreeNode(0)
cur = ans
inorder(root)
return ans.right
}
func inorder(_ node: TreeNode?) {
guard var node = node else { return }
inorder(node.left)
node.left = nil
cur?.right = node
cur = node
inorder(node.right)
}
}