230. Kth Smallest Element in a BST

題目敘述

Given the root of a binary search tree, and an integer k, return the k**th smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

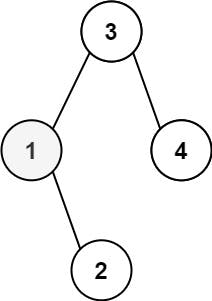
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

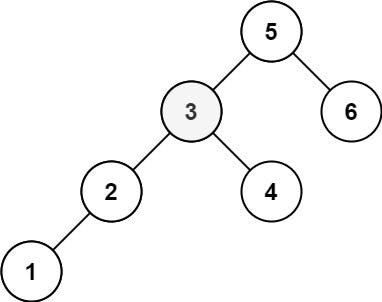
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Constraints:

• The number of nodes in the tree is n.
• 1 <= k <= n <= 10**4
• 0 <= Node.val <= 10**4

Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?

Hint 1:

Try to utilize the property of a BST.

Hint 2:

Try in-order traversal.

Hint 3:

What if you could modify the BST node's structure?

Hint 4:

The optimal runtime complexity is O(height of BST).

題目翻譯

這題目是要在一個二元搜尋樹中，第 k 個最小的數值。

解法解析

這題目算是已經可以大概知道就是有 Iteration 和 Recursion 的兩種解法。而且利用二元樹的特性，因為左側是最小值，直接先從最左側開始往回找。

解法範例

Go

Iteration

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func kthSmallest(root *TreeNode, k int) int {
    stack := []*TreeNode{}
    cur := root

    for k >= 0 {
        for cur != nil {
            stack = append(stack, cur)
            cur = cur.Left
        }

        cur = stack[len(stack)-1]
        stack = stack[:len(stack)-1]
        k--
        if k == 0 {
            return cur.Val
        }
        cur = cur.Right
    }

    return cur.Val
}

Recursion

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func kthSmallest(root *TreeNode, k int) int {
    cur := 0
    val := 0
    dfs(root, k, &cur, &val)
    return val

}

func dfs(node *TreeNode, k int, cur, val *int) {
    if node == nil {
        return
    }
    dfs(node.Left, k, cur, val)

    *cur = *cur + 1
    if *cur == k {
        *val = node.Val
    }
    dfs(node.Right, k, cur, val)
}

JavaScript

Iteration

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function (root, k) {
    const stack = [];
    let cur = root;
    while (cur || stack.length) {
        while (cur) {
            stack.push(cur);
            cur = cur.left;
        }
        cur = stack.pop();
        k--;
        if (!k) {
            return cur.val;
        }
        cur = cur.right;
    }
};

Recursion

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function (root, k) {
    let answer = 0;
    function inorder(root) {
        if (!root) return;
        inorder(root.left);
        if (--k === 0) {
            answer = root.val;
            return;
        }
        inorder(root.right);
    }
    inorder(root);
    return answer;
};

Kotlin

PHP

Python

Iteration

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        """
        :type root: TreeNode
        :type k: int
        :rtype: int
        """
        stack = []

        while True:
            while root:
                stack.append(root)
                root = root.left
            root = stack.pop()
            k -= 1
            if not k:
                return root.val
            root = root.right

Recursion

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        """
        :type root: TreeNode
        :type k: int
        :rtype: int
        """
        def inorder(r):
            return inorder(r.left) + [r.val] + inorder(r.right) if r else []

        return inorder(root)[k - 1]

Rust

Swift