Algorithm 演算法 - 判圈系列 Floyd判圈算法(龜兔賽跑算法)
Floyd Cycle Detection Algorithm(Tortoise and Hare Algorithm)
簡介 Intro
該算法據高德納稱由美國科學家羅伯特·弗洛伊德發明,但這一算法並沒有出現在羅伯特·弗洛伊德公開發表的著作。一個可以在有限狀態機、迭代函數或者鍊表上判斷是否存在環,求出該環的起點與長度的算法。
演算法解釋
下圖是這整個演算法的邏輯思維流程圖
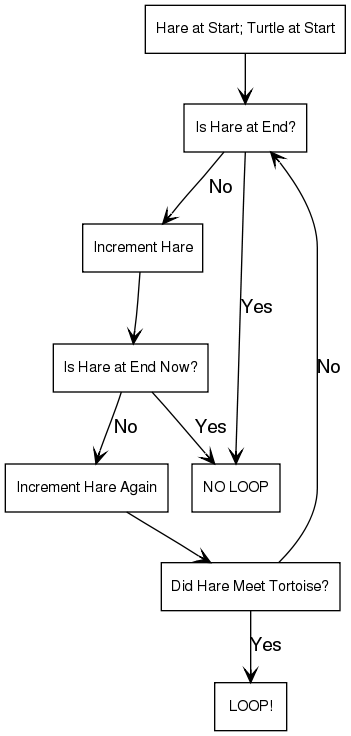
演算法可以算是一種 Two-Pointer 的解法,可以想像在操場上跑步,在一個環當中,一個跑比較慢一個跑比較快,快的一定會追上慢的,以這個概念來判斷是否存在迴圈。
範例會用以下的圖作參考
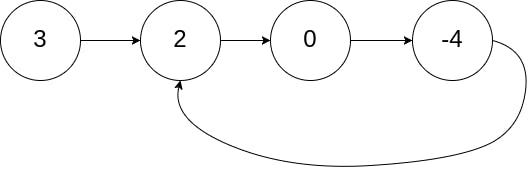
烏龜是 t 每次走一步、兔子是 r 每次走兩步。
t和r從 3 開始出發t到 2、r到 0t到 0、r到 2t到 -4、r到 -4 =>相遇了,所以判斷有迴圈存在
而如果不存在迴圈的話,r 會先走到結尾沒有下一個節點,所以當 r = null 的時候就知道迴圈不存在了。因為使用 Two-Pointer 的方式所以空間複雜度就只需要常數而已,而時間複雜度只有 O(n),n 是節點數
程式範例可以參考:LeetCode Solution, Easy, 141. Linked List Cycle
進階
進階的題目就像是 LeetCode Solution, Medium, 142. Linked List Cycle II 是要找出迴圈的連接點。
延續上面的範例,c 是迴圈的長度、l 是起點到迴圈連接點的長度、x 是連接點到第一次相遇點的長度。 從第一次相遇點的位置到連接點 f = c - x
r = l + x + n * c // c 會乘上 n 是因為在遇到 t 之前不確定已經先走了幾圈
t = l + x
l + x + n * c = 2 * (l + x) // r 每次走兩步, t 只走一步,所以總長上 r 會走 t 的兩倍
l + x + n * c = 2 * l + 2 * x
n * c = l + x // 簡化的結果,從起始點到相遇點是迴圈的倍數
l + x = (n - 1) * c + c
l + x = (n - 1) * c + f + x
l = (n - 1) * c + f
最後的結果 l = (n - 1) * c + f 可以看到 l 和 f 的長度就只差在迴圈長度的倍數,所以當今天常數 n = 1,就可以發現 l = f 了,因此當同時有兩個人分別從起點和相遇點開始走時,最後會在連接點相遇,由此找出連接點在哪。
